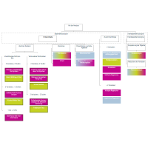
Es gibt eine sehr grosse Anzahl Verfahren, mit denen Mittelwertsunterschiede untersucht werden können. Bei der Auswahl des Verfahrens ist es wichtig zu beachten, ob die Stichproben unabhängig oder verbunden sind. Ist diese Frage geklärt, so stellt sich die Frage, wie viele verschiedene Variablen untersucht werden sollen. Zudem unterscheiden sich die Verfahren darin, ob die untersuchten Variablen normalverteilt sein sollten oder nicht.
1. Unabhängige Stichproben
1.1. Zwei Variablen, zwei Stufen
1.1.1. t-Test für unabhängige Stichproben
1.1.2. Mann-Whitney U-Test
1.2. Zwei Variablen, mehr als 2 Stufen
1.2.1. Einfaktorielle Varianzanalyse
1.2.2. Kruskal-Wallis
1.3. Eine abhängige Variable, mehr als zwei unabhängige Variablen
1.3.1. Mehrfaktorielle Varianzanalyse
2. Verbundene Stichproben
2.1. Zwei Variablen, zwei Stufen
2.1.1. t-Test für verbundene Stichproben
2.1.2. Wilcoxon-Test
2.1.3. Vorzeichentest
2.2 Zwei Variablen, mehr als 2 Stufen
2.2.1. Einfaktorielle Varianzanalyse mit Messwiederholung
2.2.2. Friedman-Test
1. Unabhängige Stichproben
Von unabhängigen Stichproben (Gruppen) spricht man, wenn die Mittelwerte zweier nicht zusammenhängender Stichproben miteinander verglichen werden. Dies ist beispielsweise dann der Fall, wenn das mittlere Einkommen einer Zufallsstichprobe von Ärzten mit dem mittleren Einkommen einer Zufallsstichprobe von Anwälten verglichen wird. Ein typisches Beispiel ist auch, wenn die Mittelwerte von Männern und Frauen verglichen werden. In den meisten Anwendungsgebieten sind unabhängige Stichproben der Normalfall, während verbundene Stichproben eher selten sind (z.B. wenn Paare oder Zwillinge befragt werden).
Es gibt eine Reihe von Verfahren, mit denen die Mittelwertsunterschiede zwischen zwei oder mehr unabhängigen Stichproben auf Signifikanz untersucht werden können. Sollen zwei Mittelwerte geprüft werden, so wird der t-Test für unabhängige Stichproben oder der Mann-Whitney-U-Test eingesetzt. Sollen mehr als zwei Mittelwerte verglichen werden, so kommt eine Varianzanalyse oder ein Kruskal-Wallis-Test zum Einsatz. Soll für den Effekt einer Drittvariable kontrolliert werden, so ist beispielsweise eine mehrfaktorielle Varianzanalyse möglich. Die genannten Verfahren unterscheiden sich darin, welche Voraussetzungen sie an das Skalenniveau und die Verteilung der Daten stellen (siehe deskriptive Analyse).
1.1. Zwei Variablen, zwei Stufen
Diese Tests vergleichen zwei Stichproben (Gruppen) miteinander (daher „2 Stufen“, z.B. Männer und Frauen, Placebo und Treatment) bezüglich eines Mittelwerts auf einer abhängigen Variable. Das heisst, es sind zwei Variablen involviert: die Gruppierungsvariable, die besagt, zu welcher Stichprobe eine Person gehört und eine abhängige Variable, auf der nach Unterschieden gesucht wird (z.B. Einkommen, Knochendichte etc.). Die Wahl des richtigen Tests hängt vom Skalenniveau und von der Verteilung der abhängigen Variablen ab.
1.1.1. t-Test für unabhängige Stichproben
Mittels eines t-Tests könnte also untersucht werden, ob es zwischen zwei verschiedenen Schulklassen Unterschiede im Mittelwerts der Gedächtnisleistung der Schüler gibt. t-Test für unabhängige Stichproben
1.1.2 Mann-Whitney-U-Test (auch Wilcoxon Rangsummentest)
Mittels eines Mann-Whitney-U-Tests können die Unterschiede der zentralen Tendenz einer mindestens ordinalskalierten Variablen zwischen zwei unabhängigen Stichproben untersucht werden. Die Daten müssen dabei nicht normalverteilt sein. Mit einem Mann-Whitney-U-Test kann folgender Untersuchungsplan analysiert werden:
Mit dem Mann-Whitney-U-Tests könnte also untersucht werden, ob es zwischen zwei Schulklassen Unterschiede in der zentralen Tendenz der Schulnoten gibt. Mann-Whitney-U-Test
1.2. Zwei Variablen, mehr als 2 Stufen
Sollen mehr als zwei Stichproben hinsichtlich ihrer Mittelwertsunterschiede untersucht werden (daher „mehr als zwei Stufen“, zum Beispiel Placebo, geringe Dosis, mittlere Dosis, hohe Dosis), wird entweder eine einfaktorielle Varianzanalyse oder ein Kruskal-Wallis-Test verwendet. Das heisst, es sind zwei Variablen involviert: die Gruppierungsvariable, welche aussagt, zu welcher Stichprobe eine Person gehört, und eine abhängige Variable, auf welcher nach Unterschieden gesucht wird (z.B. Einkommen, Knochendichte etc.). Die Wahl des richtigen Tests hängt vom Skalenniveau und von der Verteilung der abhängigen Variablen ab.
1.2.1. Einfaktorielle Varianzanalyse
Mit einer einfaktoriellen Varianzanalyse können die Mittelwertsunterschiede einer normalverteilten, intervallskalierten Variablen zwischen mehr als zwei unabhängigen Stichproben untersucht werden. Mit einer Varianzanalyse könnte das folgende Modell auf Mittelwertsunterschiede zwischen den Stichproben untersucht werden:
Mittels einer einfaktoriellen Varianzanalyse könnte also untersucht werden, ob es zwischen drei verschiedenen Schulklassen Unterschiede bezüglich des Mittelwertes der Gedächtnisleistung gibt. Einfaktorielle Varianzanalyse
1.2.2. Kruskal-Wallis Test
Mittels eines Kruskal-Wallis-Tests können die Unterschiede der zentralen Tendenz einer Variablen zwischen mehr als zwei unabhängigen Stichproben untersucht werden. Die abhängige Variable muss dabei nicht normalverteilt sein. Das folgende Modell lässt sich mit einem Kruskal-Wallis-Test untersuchen:
Durch einen Kruskal-Wallis-Test lässt sich der Unterschied in der zentralen Tendenz der Schulnoten von drei Schulklassen untersuchen. Kruskal-Wallis-Test
1.3. Eine abhängige Variable, mehr als zwei unabhängige Variablen
Soll der Einfluss von mehr als einer Variable (daher „mehr als eine unabhängige Variable“, z.B. Autokategorie, Autofarbe, Händler) auf den Mittelwert einer abhängigen Variablen (z.B. Verkaufspreis) untersucht werden, so kann eine mehrfaktorielle Varianzanalyse durchgeführt werden, sofern die Voraussetzungen erfüllt sind.
1.3.1. Mehrfaktorielle Varianzanalyse
Mittels einer mehrfaktoriellen Varianzanalyse können die Mittelwertsunterschiede einer normalverteilten, intervallskalierten Variablen hinsichtlich mehrerer unabhängiger Variablen untersucht werden. Das folgende Modell lässt sich mit einer mehrfaktoriellen Varianzanalyse auf signifikante Mittelwertsunterschiede untersuchen:
Bei diesem Untersuchungsplan handelt es sich um ein 2×2-Design. Es gibt zwei Stichprobenvariablen (Schulklasse & Geschlecht), die jeweils zwei Abstufungen haben, woraus sich insgesamt 4 Stichproben ergeben, die auf Mittelwertsunterschiede untersucht werden. Es gibt keine Grenze bei der Anzahl von Variablen oder Abstufungen, lediglich die Stichprobengrösse muss hinreichend sein. Mehrfaktorielle Varianzanalyse
2. Verbundene Stichproben
Wird die gleiche Variable zweimal bei derselben Stichprobe erhoben, beispielsweise vor und nach einer Intervention, so spricht man von abhängigen bzw. verbundenen Stichproben oder Daten.
Es gibt eine Reihe von Verfahren, mit denen Mittelwertsunterschiede zwischen zwei oder mehreren verbundenen Stichproben auf Signifikanz untersucht werden können.Liegen zwei Gruppen vor, so empfehlen sich der t-Test für abhängige Stichproben sowie der Wilcoxon-Test oder der Vorzeichentest. Liegen mehr als zwei Gruppen vor, so empfiehlt sich eine einfaktorielle Varianzanalyse mit Messwiederholung oder alternativ ein Friedman-Test. Soll für den Effekt einer Drittvariable kontrolliert werden, so ist beispielsweise eine mehrfaktorielle Varianzanalyse mit Messwiederholung möglich. Die Verfahren unterscheiden sich darin, welche Voraussetzungen sie an das Skalenniveau und die Verteilung der Daten stellen (siehe deskriptive Analyse).
2.1. Zwei Variablen, zwei Stufen
Diese Tests vergleichen zwei Stichproben (Gruppen) miteinander (daher „2 Stufen“, z.B. Ehemann und Ehefrau, Zwilling A und Zwiling B) bezüglich eines Mittelwerts auf einer abhängigen Variablen. Das heisst, es sind zwei Variablen involviert: die Messung bei der einen Stichprobe und die Messung bei der anderen Stichprobe (daher „zwei Variablen“). Die Wahl des richtigen Tests hängt vom Skalenniveau und von der Verteilung der abhängigen Variablen ab.
2.1.1. t-Test für verbundene Stichproben
Mit einem t-Test können die Mittelwertsunterschiede einer normalverteilten, intervallskalierten Variablen zwischen zwei verbundenen Stichproben untersucht werden. Das Versuchsdesign in Abbildung 6 könnte beispielsweise mit einem t-Test für verbundene Stichproben untersucht werden.
Mit diesem Versuchsdesign lässt sich der Einfluss von sogenanntem Powernapping auf die Gedächtnisleistung untersuchen. Die Schulklasse nimmt zunächst an einem Gedächtnistest teil. An einem zweiten Tag wird zuerst ein Powernapping und dann erneut der Gedächtnistest durchgeführt. Anschliessend werden die Mittelwerte der beiden Gedächtnistests mit dem t-Test auf signifikante Unterschiede getestet. Da dieselbe Stichprobe getestet wird, handelt es sich um verbundene Daten bzw. Stichproben. t-Test für verbundene Stichproben
2.1.2. Wilcoxon-Test
Mittels eines Wilcoxon-Tests (auch „Wilcoxon signed-rank test“) können die Unterschiede der zentralen Tendenz einer mindestens ordinalskalierten Variablen zwischen zwei verbundenen Stichproben untersucht werden. Die Variablen müssen nicht normalverteilt sein. Mit einem Wilcoxon-Test kann das folgende Versuchsdesign analysiert werden:
Durch diese Analyse lässt sich untersuchen, ob eine „aktive Pause“, bei der die Schüler motiviert werden, in der Schulpause eine körperlichen Aktivität auszuüben, einen Einfluss auf das Gewicht hat. Da dieselbe Schulklasse zweimal untersucht wird, handelt es sich um verbundene Daten bzw. Stichproben. Wilcoxon-Test
2.1.3. Vorzeichentest
Mittels eines Vorzeichentests können die Unterschiede der zentralen Tendenz einer mindestens ordinalskalnierten Variablen zwischen zwei verbundenen Stichproben untersucht werden. Die Variablen müssen nicht normalverteilt sein. Das folgende Versuchsdesign könnte mit dem Vorzeichentest analysiert werden:
Mit einem solchen Design lässt sich untersuchen, ob die Zufriedenheit mit dem Lehrer dann zunimmt, wenn dieser eine Fortbildung besucht. Auch hier handelt es sich um verbundene Stichproben bzw. Daten, da dieselbe Schulklasse zwei Mal befragt wird. Vorzeichentest
2.2. Zwei Variablen, mehr als 2 Stufen
Sollen mehr als zwei verbundene Stichproben hinsichtlich ihrer Mittelwertsunterschiede untersucht werden (daher „mehr als zwei Stufen“), wird entweder eine einfaktorielle Varianzanalyse mit Messwiederholung oder ein Friedman-Test verwendet. Die Wahl des richtigen Tests hängt vom Skalenniveau und von der Verteilung der abhängigen Variablen ab.
2.2.1. Einfaktorielle Varianzanalyse mit Messwiederholung
Mittels einer einfaktoriellen Varianzanalyse mit Messwiederholung können die Mittelwertsunterschiede einer normalverteilten, intervallskalierten Variablen zwischen mehr als zwei verbundenen Stichproben untersucht werden. Folgendes Versuchsdesign könnte bezüglich der Mittelwertsunterschiede zwischen einzelnen Messzeitpunkten untersucht werden:
Das Design untersucht und vergleicht die Lernfähigkeit von Schülern vor, direkt nach und 6 Wochen nach dem Training. Einfaktorielle Varianzanalyse mit Messwiederholung
2.2.2. Friedman-Test
Mittels eines Friedman-Tests können Unterschiede der zentralen Tendenz einer mindestens ordinalskalierten Variablen zwischen mehr als zwei verbundenen Stichproben untersucht werden. Die Variablen müssen nicht normalverteilt sein. Folgendes Versuchsdesign lässt sich mittels eines Friedman-Tests untersuchen:
Es wird die Zufriedenheit mit dem Lehrer vor, direkt nach und 6 Wochen nach einer Fortbildung untersucht und verglichen. Friedman-Test

