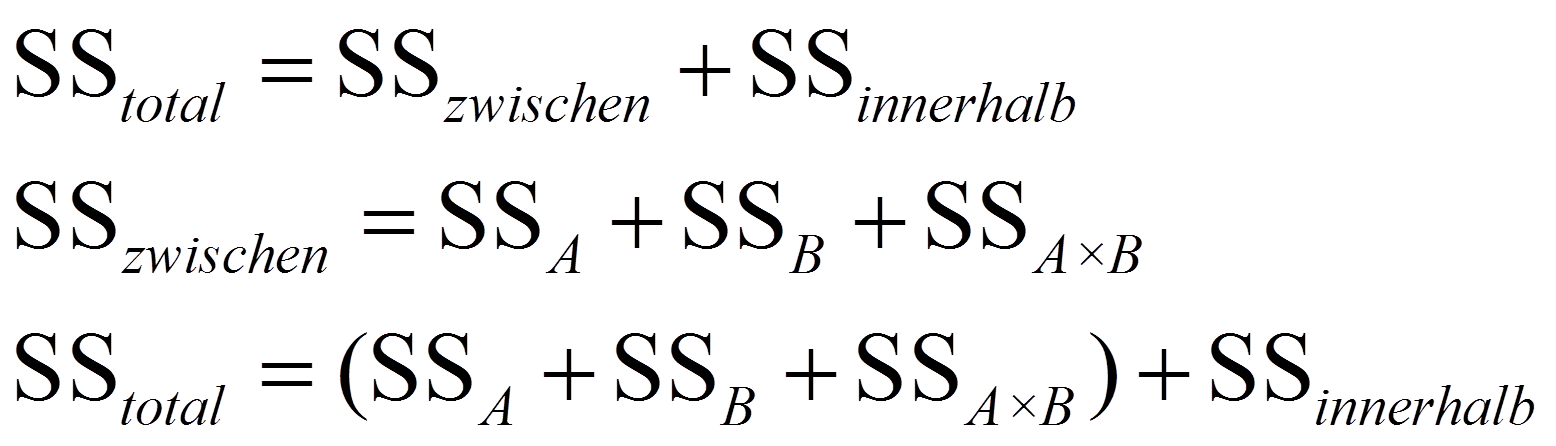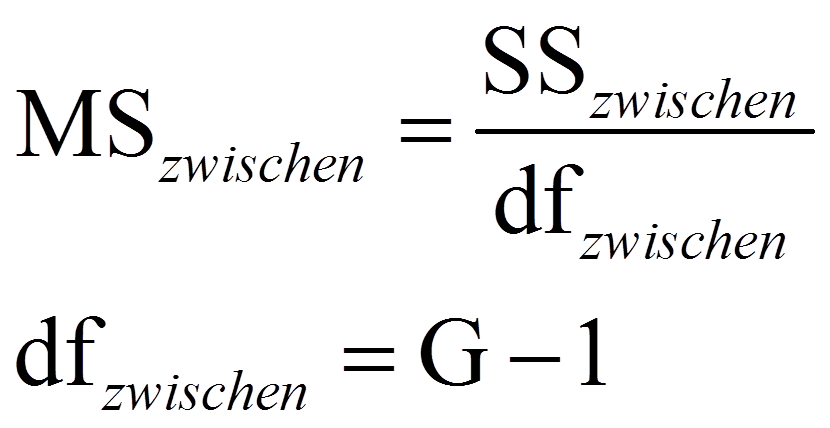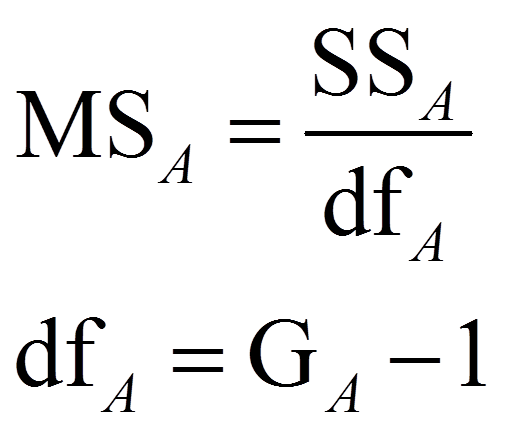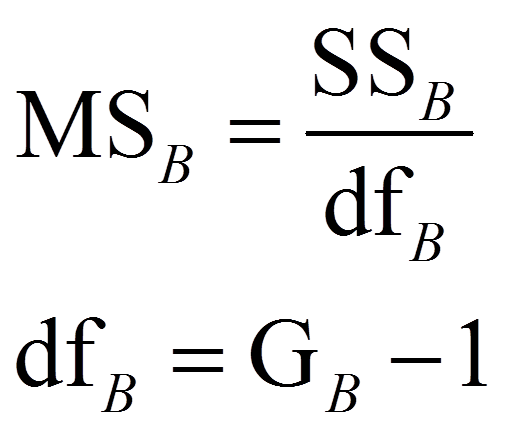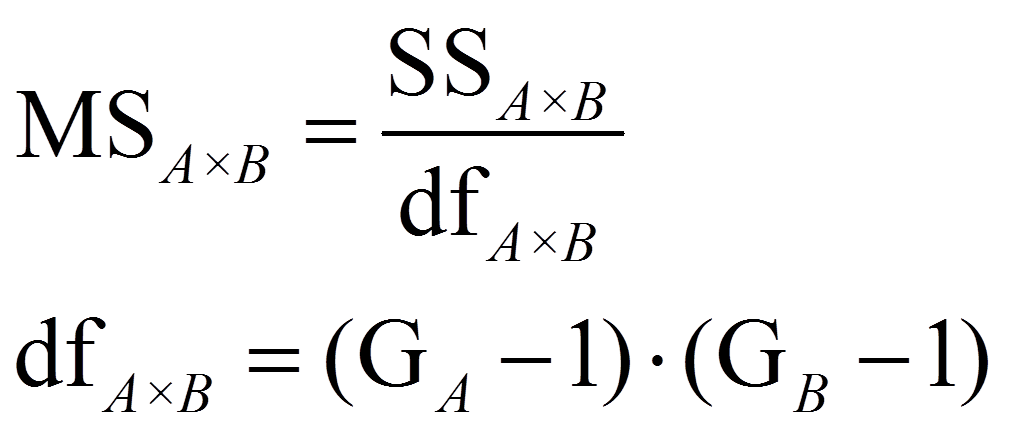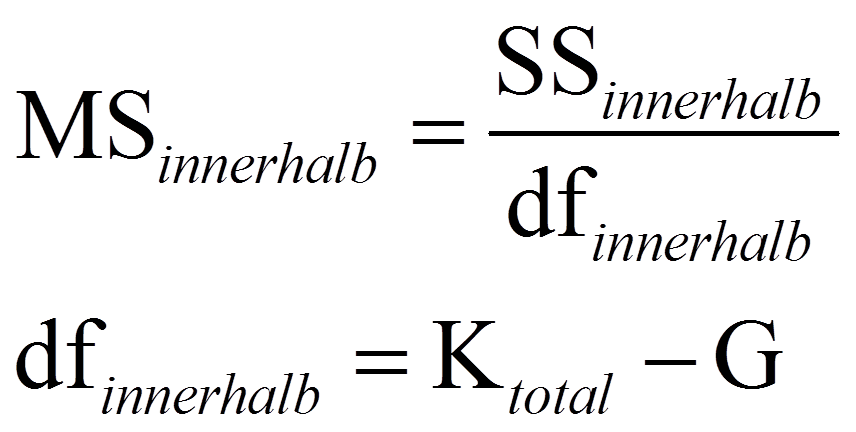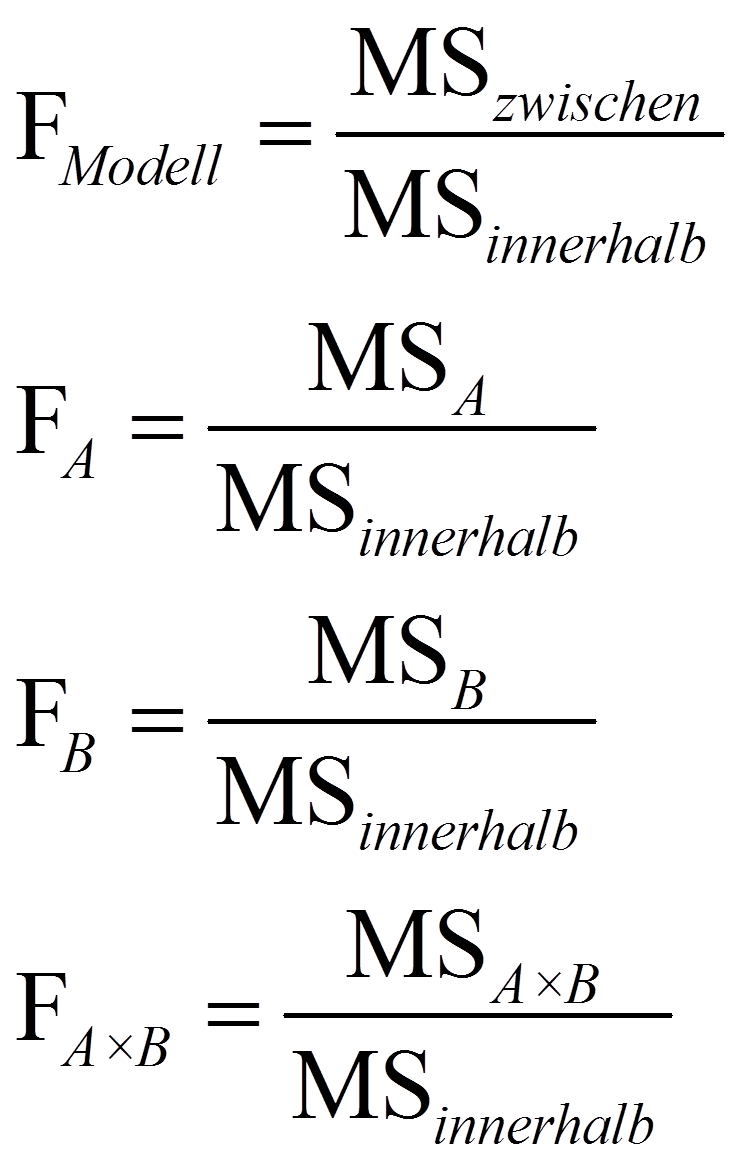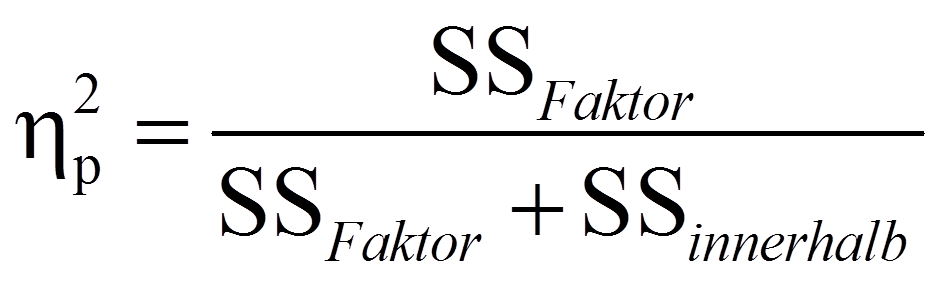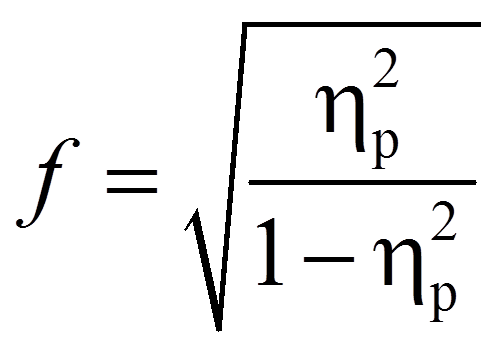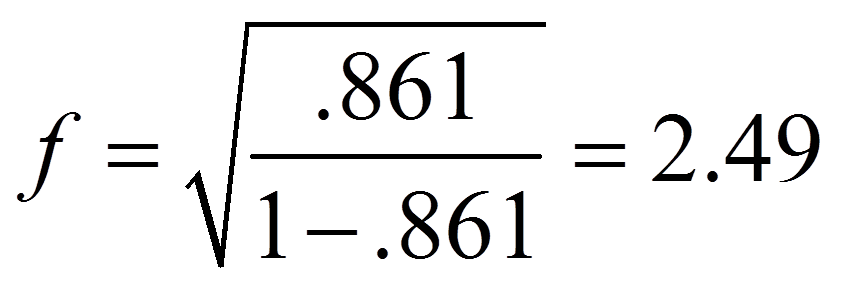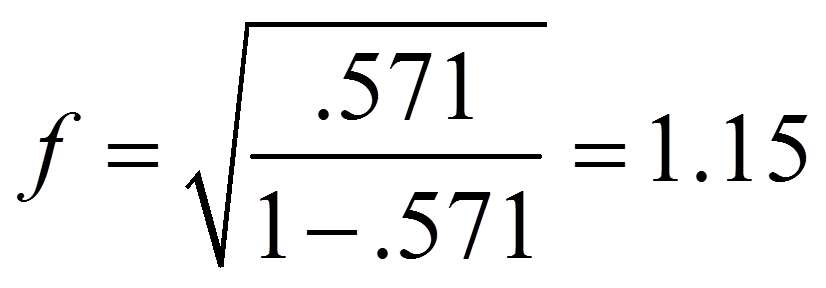 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen der einfaktoriellen Varianzanalyse
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Die Grundidee der Varianzanalyse
2.3. Berechnung der Teststatistik
3. Die mehrfaktorielle Varianzanalyse mit SPSS
3.1. SPSS-Befehle
3.2. Prüfung der Varianzhomogenität (Levene-Test)
3.3. Ergebnisse der mehrfaktoriellen Varianzanalyse
3.4. Post-hoc-Tests
3.5. Profildiagramme
3.6. Berechnung der Effektstärke
3.7. Eine typische Aussage
Quick Start
| Wozu wird die mehrfaktorielle Varianzanalyse verwendet? Die mehrfaktorielle Varianzanalyse testet, ob sich die Mittelwerte mehrerer unabhängiger Gruppen (oder Stichproben), die durch mehrere kategoriale unabhängige Variable definiert werden, unterscheiden. SPSS-Menü
Analysieren > Allgemeines Lineares Modell > Univariat SPSS-Syntax
UNIANOVA abhängige Variable BY Faktor_1 Faktor_2 … /METHOD=SSTYPE(3) /INTERCEPT=INCLUDE /POSTHOC= Faktor 1 Faktor …(BONFERRONI) /PLOT=PROFILE(Faktor_1*Faktor_2, Faktor_2*Faktor_1 …) /PRINT=ETASQ HOMOGENEITY DESCRIPTIVE /CRITERIA=ALPHA(.05) /DESIGN=Faktor_1 Faktor_2 Faktor_1*Faktor_2 …. SPSS-Beispieldatensatz
Mehrfaktorielle Varianzanalyse |
1. Einführung
Die mehrfaktorielle Varianzanalyse testet, ob sich die Mittelwerte mehrerer unabhängiger Gruppen (oder Stichproben), die durch mehrere kategoriale unabhängige Variable definiert werden, unterscheiden.
Diese unabhängigen Variablen werden im Kontext der Varianzanalyse als „Faktoren“ bezeichnet. Entsprechend werden die Ausprägungen der unabhängigen Variable „Faktorstufen“ genannt, wobei auch der Begriff der „Treatments“ gebräuchlich ist. Als „mehrfaktoriell“ wird eine Varianzanalyse bezeichnet, wenn sie mehr als einen Faktor, also mehrere Gruppierungsvariablen, verwendet (vgl. einfaktorielle Varianzanalyse). Der Begriff „Varianzanalyse“ wird wie bei allen Varianzanalysen oft mit „ANOVA“ abgekürzt, da sie in Englisch mit „Analysis of variance“ bezeichnet wird.
Das Prinzip der Varianzanalyse besteht in der Zerlegung der Varianz der abhängigen Variable. Die Gesamtvarianz setzt sich aus der sogenannten „Varianz innerhalb der Gruppen“ und der „Varianz zwischen den Gruppen“ zusammen. Bei einer mehrfaktoriellen Varianzanalyse wird die Varianz zwischen den Gruppen weiter aufgegliedert, und zwar in die Varianz der einzelnen Faktoren und die Varianz der Interaktion(en) der Faktoren. Im Rahmen einer Varianzanalyse wird die Varianz zwischen den Gruppen mit der Varianz innerhalb der Gruppen verglichen.
Die Fragestellung der mehrfaktoriellen Varianzanalyse wird oft so verkürzt: „Unterscheiden sich die Mittelwerte einer abhängigen Variable zwischen mehreren Gruppen? Welche Faktorstufen unterscheiden sich? Gibt es Interaktionseffekte?“
1.1. Beispiele für mögliche Fragestellungen
- Welchen Einfluss haben die politische Orientierung (links, mitte-links, mitte-rechts, rechts), die Bildung (tief, mittel, hoch) und die soziale Schicht (tief, mittel, hoch) auf die Einstellung zur Liberalisierung von Marihuana?
- Haben Produktionsort (Inland, Ausland) und Label (Bio-Label, Fair-Trade-Label, kein Label) einen Einfluss auf die verkaufte Menge von getrockneten Aprikosen? Gibt es eine Interaktion, zum Beispiel in dem Sinne, dass sich ein „Bio-Label“ bei inländischer Produktion günstiger auswirken würde?
- In einem Experiment zur sozialen Kooperation werden vier Faktoren manipuliert: die Anonymität der Personen (vollständige, teilweise, keine), die Anonymität der Entscheidungen (vollständige, teilweise, keine), die Gruppengrösse (3, 4, 5, 6 Personen) sowie die Verfügbarkeit von Sanktionsmöglichkeiten (ja, nein). Wie beeinflussen diese Faktoren die Kooperationshäufigkeit?
1.2. Voraussetzungen der einfaktoriellen Varianzanalyse
| ✓ | Die abhängige Variable ist intervallskaliert |
| ✓ | Die unabhängigen Variablen (Faktoren) sind kategorial (nominal- oder ordinalskaliert) |
| ✓ | Die durch die Faktoren gebildeten Gruppen sind unabhängig |
| ✓ | Die abhängige Variablen ist normalverteilt innerhalb jeder der Gruppen. Ab 25 Probanden pro Gruppe sind Verletzungen dieser Voraussetzung unproblematisch |
| ✓ | Homogenität der Varianzen: Die Gruppen stammen aus Grundgesamtheiten mit annähernd identischen Varianzen der abhängigen Variablen (siehe Levene-Test) |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
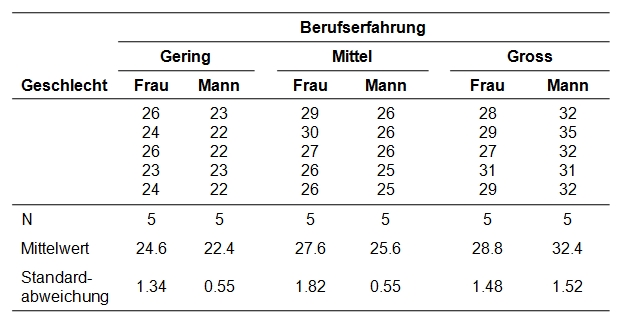
In einer Umfrage wurden 30 Studierende nach der Höhe ihres Lohns (Stundenlohn) befragt. Zusätzlich wurden zwei mögliche Einflussfaktoren erhoben: die Berufserfahrung (3 Erfahrungsstufen) und das Geschlecht. Haben Arbeitserfahrung und Geschlecht einen Einfluss auf den Lohn? Liegt eine Interaktion zwischen Arbeitserfahrung und Geschlecht vor?
Der zu analysierende Datensatz enthält neben einer Personennummer (ID) den Stundenlohn (Stundenlohn) sowie die Gruppierungsvariablen Berufserfahrung (gering, mittel, gross) und Geschlecht (männlich, weiblich).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Die Grundidee der Varianzanalyse
Ein Blick auf die Gruppenmittelwerte der Beispieldaten (Abbildung 1) zeigt, dass sich die Mittelwerte unterscheiden. Um zu überprüfen, ob die Unterschiede signifikant sind, wird eine Varianzanalyse durchgeführt. In der Einführung zur einfaktoriellen Varianzanalyse wird knapp in die Grundidee der Varianzanalyse eingeführt. Daher wird an dieser Stelle auf eine Wiederholung verzichtet und es wird lediglich auf einige Unterschiede aufmerksam gemacht.
Zerlegung der individuellen Messwerte
Im Unterschied zur einfaktoriellen Varianzanalyse wird hier der Effekt der Gruppenzugehörigkeiten weiter aufgeteilt, da mehr als ein Faktor vorliegt: Es wird jedem der Faktoren und jeder Interaktion zwischen den Faktoren ein Anteil zugeordnet. Damit ist ein ebenfalls neues Thema angesprochen: Interaktionseffekte.
Haupteffekte und Interaktionseffekte
Der direkte Effekt eines Faktors auf die abhängige Variable wird als Haupteffekt bezeichnet. Im Beispiel sind dies der Haupteffekt der Berufserfahrung und der Haupteffekt des Geschlechts. Eine Interaktion zweier Faktoren dagegen bedeutet, dass die beiden Faktoren in komplexer Weise zusammenwirken. Dies ist nicht rein additiv zu verstehen. Liegt eine Interaktion vor, so ist die Wirkung des einen Faktors abhängig von der Ausprägung des anderen Faktors und umgekehrt. Im Beispiel gesprochen hiesse dies, dass der Effekt des Geschlechts auf den Lohn sich je nach Berufserfahrung unterscheidet, und umgekehrt, dass der Effekt der Berufserfahrung je nach Geschlecht unterschiedlich ausfiele.
SPSS schliesst automatisch alle möglichen Interaktionen in das Modell mit ein: Bei zwei Faktoren A und B ist dies die Interaktion A x B. Bei drei Faktoren A, B und C sind dies die Interaktion A x B, A x C, B x C sowie die Dreifachinteraktion A x B x C.
Quadratsummen
Wie bereits bei der einfaktoriellen Varianzanalyse erläutert, wird die Gesamtvariation zerlegt in die Variation zwischen den Gruppen und die Variation innerhalb der Gruppen. Zusätzlich wird die Variation zwischen den Gruppen (SSzwischen) noch weiter aufgeteilt: Jedem Faktor und jeder Interaktion wird eine Quadratsumme zugeteilt. Liegen beispielsweise zwei Faktoren, A und B, vor, so gilt:
2.3. Berechnung der Teststatistik
Berechnen der Teststatistik
Um die Teststatistik F zu berechnen, werden die mittleren Quadratsummen MSzwischen und MSinnerhalb (respektive MSA, MSB, MSAxB) benötigt („MS“ da engl. „mean squares“). Dazu werden die Quadratsummen durch ihre jeweiligen Freiheitsgrade dividiert:
mit
| = | Stichprobengrösse über alle Gruppen hinweg (im vorliegenden Beispiel: Ktotal = 30) | |
| = | Anzahl Faktorstufen (im vorliegenden Beispiel: 2 Geschlechter, 3 Levels der Berufserfahrung) |
Anschliessend werden die Teststatistiken F für das Gesamtmodell, den Faktor A, den Faktor B und die Interaktion A x B folgendermassen berechnet:
Signifikanz der Teststatistik
Je mehr Varianz das Modell (respektive ein Faktor oder die Interaktion) erklärt, desto höher fällt der jeweilige F-Wert aus, denn über dem Bruchstrich steht ein Mass für die erklärte Varianz, während unter dem Bruchstrich ein Mass für die Residualvarianz des Modells verwendet wird. Die resultierenden F-Werte werden mit den jeweiligen kritischen Werten auf einer durch die Freiheitsgrade dfzwischen (respektive dfA, dfB oder dfAxB) und dfinnerhalb charakterisierten F-Verteilung verglichen. Ist der F-Wert höher als der kritische Wert, so ist der Test signifikant.
3. Die mehrfaktorielle Varianzanalyse mit SPSS
3.1. SPSS-Befehle
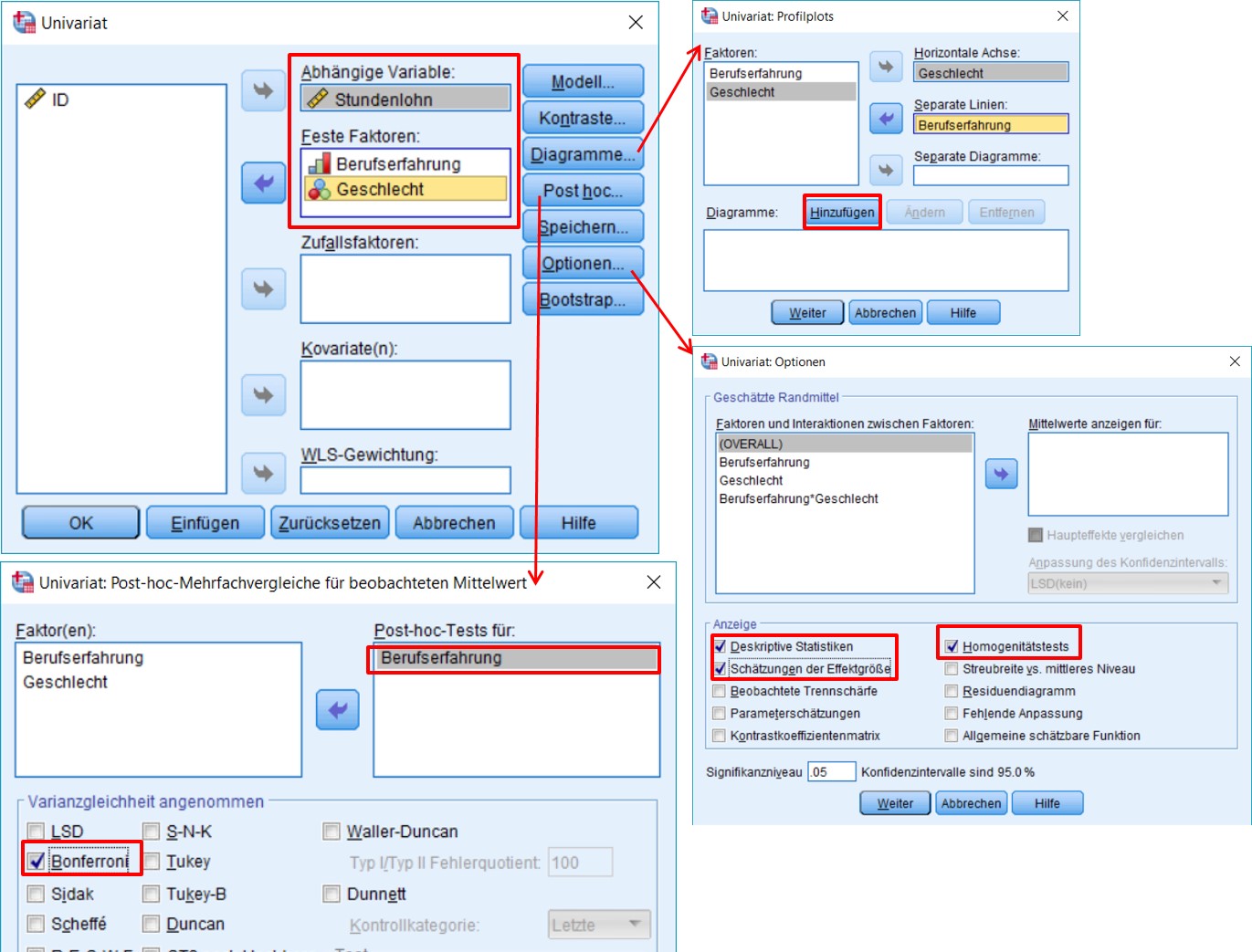
SPSS-Menü: Analysieren > Allgemeines Lineares Modell > Univariat
Hinweis
- Für den Faktor Geschlecht sind keine Post-hoc-Tests nötig, da dieser nur zwei Stufen hat.
SPSS-Syntax
UNIANOVA Stundenlohn BY Berufserfahrung Geschlecht
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=Berufserfahrung (BONFERRONI)
/PLOT=PROFILE(Berufserfahrung*Geschlecht, Geschlecht*Berufserfahrung)
/PRINT=ETASQ HOMOGENEITY DESCRIPTIVE
/CRITERIA=ALPHA(.05)
/DESIGN=Berufserfahrung Geschlecht Berufserfahrung*Geschlecht.
3.2. Prüfung der Varianzhomogenität (Levene-Test)
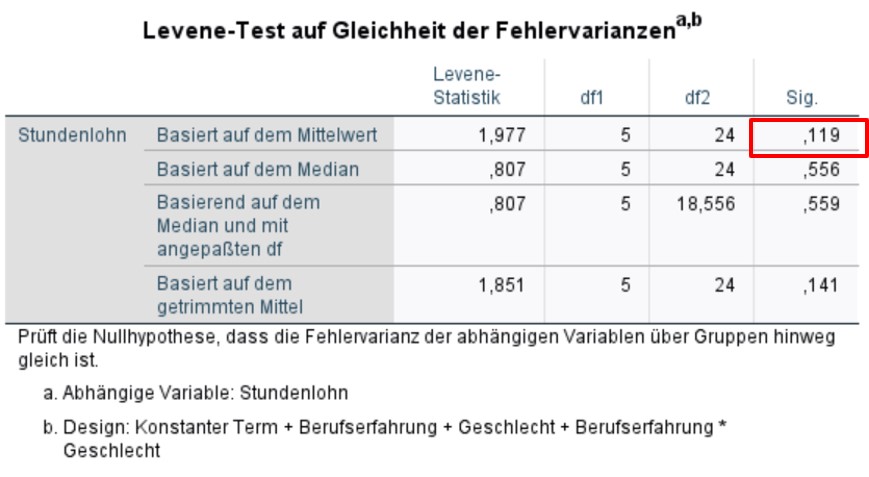
Der Levene-Test prüft die Nullhypothese, dass die Varianzen der Gruppen sich nicht unterscheiden. Ist der Levene-Test nicht signifikant, so kann von homogenen Varianzen ausgegangen. Wäre der Levene-Test jedoch signifikant, so wäre eine der Grundvoraussetzungen der Varianzanalyse verletzt. Gegen leichte Verletzungen gilt die Varianzanalyse als robust; vor allem bei genügend und etwa gleich grossen Gruppen sind Verletzungen nicht problematisch. Bei ungleich grossen Gruppen führt eine starke Verletzung der Varianzhomogenität zu einer Verzerrung des F–Tests. Alternativ kann dann auf den Brown-Forsythe-Test oder den Welch-Test zurückgegriffen werden. Dabei handelt es sich um adjustierte F-Tests. In SPSS sind diese derzeit nur für einfaktorielle Varianzanalysen implementiert, wenn diese über das Menü Analysieren > Mittelwerte vergleichen > Einfaktorielle ANOVA durchgeführt werden (unter „Optionen“).
Im vorliegenden Beispiel ist der Levene-Test nicht signifikant (F(5,24) = 1.977, p = .119), so dass von Varianzhomogenität ausgegangen werden kann.
3.3. Ergebnisse der mehrfaktoriellen Varianzanalyse
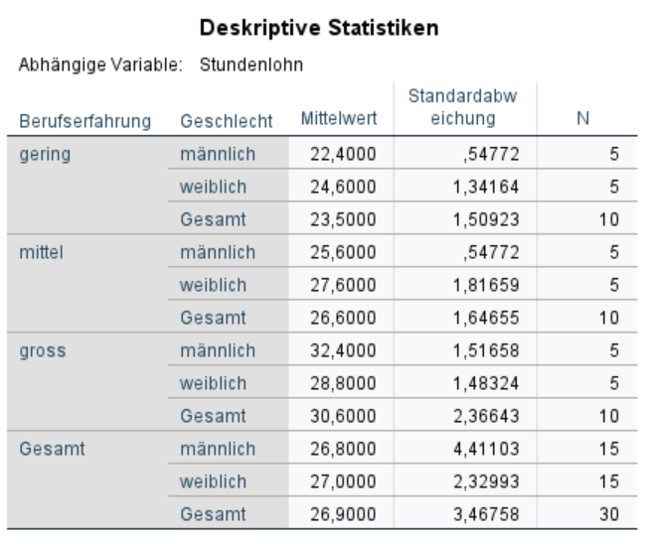
Die Tabelle in Abbildung 4 gibt die Mittelwerte, Standardabweichungen und Grössen aller sechs Subgruppen wieder. Sechs Gruppen sind es, da ein 2 x 3 – Design vorliegt (2 Geschlechter, 3 Levels der Berufserfahrung). Diese Informationen werden für die Berichterstattung verwendet.
Signifikanz des Gesamtmodells und Modellgüte
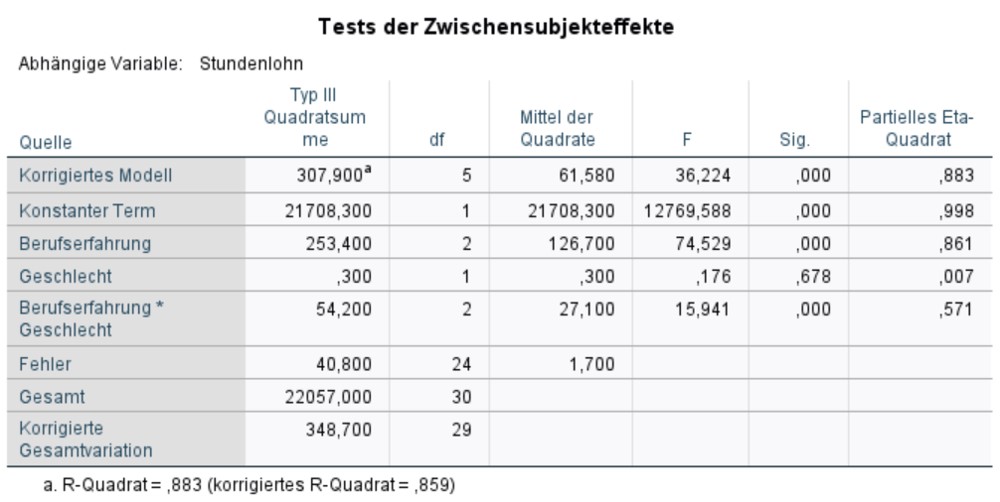
Abbildung 5 zeigt die F-Tests, die bereits im Kapitel Berechnung der Teststatistik vorgestellt wurden. In der Zeile „Korrigiertes Modell“ ist der Test für das Gesamtmodell. Der Test ist signifikant. Dies bedeutet, das Gesamtmodell ist signifikant (F(5,24) = 36.22, p < .001).
Als Fussnote beinhaltet Abbildung 5 zudem ein Mass für die Modellgüte: das korrigierte R2. Dieses ist stets im Bereich von 0 bis 1 und gibt an, welcher Anteil der Streuung um den Gesamtmittelwert durch das Modell erklärt werden kann. Im vorliegenden Beispiel ist das korrigierte R2 = .859. Dies bedeutet, dass das Modell 85.9% der Streuung um den Gesamtmittelwert erklärt.
Signifikanz der Haupteffekte und der Interaktion
Wie Abbildung 5 entnommen werden kann, gibt es einen Haupteffekt der Berufserfahrung auf den Stundenlohn (F(2,24) = 74.53, p < .001, ηp2 = .861). Das bedeutet, dass Studierende in Abhängigkeit von der Berufserfahrung einen unterschiedlich hohen Stundenlohn erhalten. Für den Faktor Geschlecht wird kein Haupteffekt ersichtlich (F(1,24) = .176, p = .678). Der Stundenlohn scheint demnach unabhängig vom Geschlecht zu sein.
Der Interaktionsterm von Berufserfahrung und Geschlecht auf den Stundenlohn ist signifikant (F(2,24) = 15.94, p < .001, ηp2 = .571). Der Effekt von Berufserfahrung hängt demnach zu einem gewissen Teil vom Geschlecht ab. Dieser Zusammenhang wird weiter unten in den Profildiagrammen (Abbildungen 7 und 8) genauer betrachtet.
Das partielle Eta-Quadrat
Das partielle Eta-Quadrat (ηp2), das am rechten Rand der Tabelle in Abbildung 5 ausgegeben wird, ist ein Mass für die Effektgrösse: Es setzt die Variation, die durch einen Faktor erklärt wird, in Bezug mit jener Variation, die nicht durch andere Faktoren im Modell erklärt wird. Das partielle Eta-Quadrat zeigt also auf, welchen Anteil der Gesamtvarianz ein einzelner Faktor erklärt:
Im vorliegenden Beispiel ist der Effekt des Geschlechts nicht signifikant. Daher wird dessen partielles Eta-Quadrat nicht betrachtet. Für die Berufserfahrung beträgt das partielle Eta-Quadrat .861. Das heisst, die Berufserfahrung erklärt 86,1% derjenigen Fehlervariation, die das Modell hätte, wäre Berufserfahrung nicht im Modell. Das partielle Eta-Quadrat der Interaktion beträgt .571 und erklärt daher 57.1% der ohne die Interaktion ungeklärten Variation.
3.4. Post-hoc-Tests
Multiples Testen und die Bonferroni-Korrektur
Ist ein Haupteffekt oder eine Interaktion signifikant, so ist zwar bestätigt, dass ein Effekt vorliegt, doch ist nach wie vor unklar, welche Faktorstufen sich unterscheiden ( wenn ein Faktor mehr als zwei Ausprägungen aufweist). Bei nur zwei Ausprägungen ist klar, dass sich eben genau diese zwei Ausprägungen voneinander unterscheiden (sonst wäre der Test nicht signifikant). Im vorliegenden Beispiel liegen ein Effekt der Berufserfahrung sowie ein Interaktionseffekt vor. Post-hoc-Tests können einfach eingesetzt werden, um zu prüfen, welche Levels der Berufserfahrung sich unterscheiden. Für die Interaktion ist dies in SPSS nicht implementiert.
Wie bereits erwähnt wurde, beinhaltet der Faktor Berufserfahrung drei Stufen. Aus dem signifikanten Haupteffekt lässt sich nicht ableiten, welche der Faktorstufen einen signifikant unterschiedlichen Einfluss auf die abhängige Variable haben. Zu diesem Zweck werden Bonferroni-korrigierte Mehrfachvergleiche berechnet.
Bei der Berechnung von Post-hoc-Tests wird im Prinzip für jede Kombination von zwei Mittelwerten ein t-Test durchgeführt. Im aktuellen Beispiel der Berufserfahrung mit drei Gruppen sind dies 3 Tests. Multiple Tests sind jedoch problematisch, da der Alpha-Fehler (die fälschliche Ablehnung der Nullhypothese) mit der Anzahl der Vergleiche steigt. Wird nur ein t-Test mit einem Signifikanzlevel von .05 durchgeführt, so beträgt die Wahrscheinlichkeit des Nicht-Eintreffens des Alpha-Fehlers 95%. Werden jedoch 3 solcher Paarvergleiche vorgenommen, so beträgt die Nicht-Eintreffens-Wahrscheinlichkeit des Alpha-Fehlers (.95)3 = .857. Um die Wahrscheinlichkeit des Eintreffens des Alpha-Fehlers zu bestimmen, wird 1 – .857 = .143 gerechnet. Die Wahrscheinlichkeit des Eintreffens des Alpha-Fehlers liegt somit bei 14.3%. Diese Fehlerwahrscheinlichkeit wird als „Familywise Error Rate“ bezeichnet.
Um dieses Problem zu beheben, kann zum Beispiel die Bonferroni-Korrektur angewandt werden. Hierbei wird α durch die Anzahl der Paarvergleiche dividiert. Im hier aufgeführten Fall ist dies .05/3 = .017. Das heisst, jeder Test wird gegen ein Niveau von .017 geprüft.
Die Bonferroni-Korrektur führt zu eher konservativen Tests bezüglich des Alpha-Fehlers, während andere Korrekturen weniger konservativ sind. SPSS bietet eine grosse Auswahl an möglichen Korrekturen (vgl. Klicksequenz in Abbildung 2).
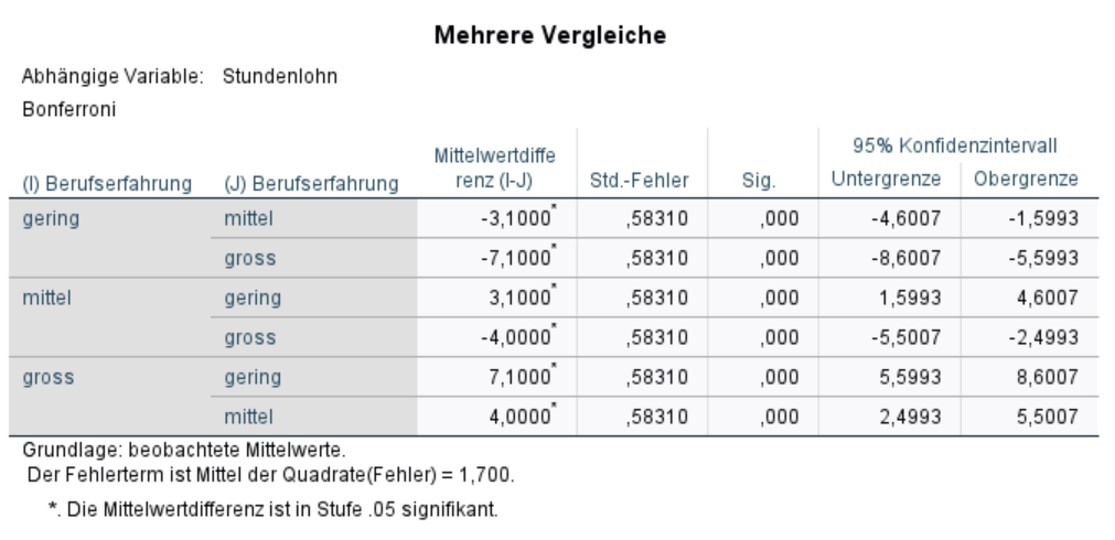
Post-hoc-Tests für den Haupteffekt der Berufserfahrung
Abbildung 6 zeigt die Ergebnisse der Post-hoc-Tests mit Bonferroni-Korrektur. In der Abbildung sind 6 und nicht nur 3 Tests aufgeführt, da SPSS jeden Test in beide Richtungen durchführt. Dies ist jedoch nicht notwendig, da das Testergebnis nicht von der Richtung abhängig ist. Ferner gilt es zu beachten, dass die p-Werte bereits von SPSS Bonferroni-korrigiert wurden und darum nun gegen .05 geprüft werden dürfen.
Es wird ersichtlich, dass sich alle Levels der Berufserfahrung signifikant voneinander unterscheiden (p < .001).
3.5. Profildiagramme
In SPSS liegen zwar keine Post-hoc-Tests für Interaktionseffekte vor, doch können Interaktionseffekte anhand von Profildiagrammen „mit getrennten Linien“ sehr gut besprochen werden. Bei einer Interaktion von zwei Faktoren können zwei verschiedene Diagramme erzeugt werden: Am Beispiel erläutert ist dies entweder ein Diagramm für Berufserfahrung mit getrennten Linien für Geschlecht (Abbildung 7, links) oder umgekehrt ein Diagramm für Geschlecht mit getrennten Linien für Berufserfahrung (Abbildung 7, rechts).
Die beiden Diagramme zeigen exakt den gleichen Sachverhalt, jedoch aus einer anderen „Perspektive“. Welches davon also betrachtet wird, spielt aus theoretischer Sicht keine Rolle. Ist eine Variable ordinal (hier: Berufserfahrung) und die andere nominal (hier: Geschlecht), so wird oft ein Diagramm erstellt, in welchem die Werte der ordinalen Variable durch Linien verbunden sind. Das heisst, die ordinale Variable wird eher für die Kategorienachse verwendet und separate Linien werden für die Werte der nominalen Variable angefordert (hier: Abbildung 7, links).
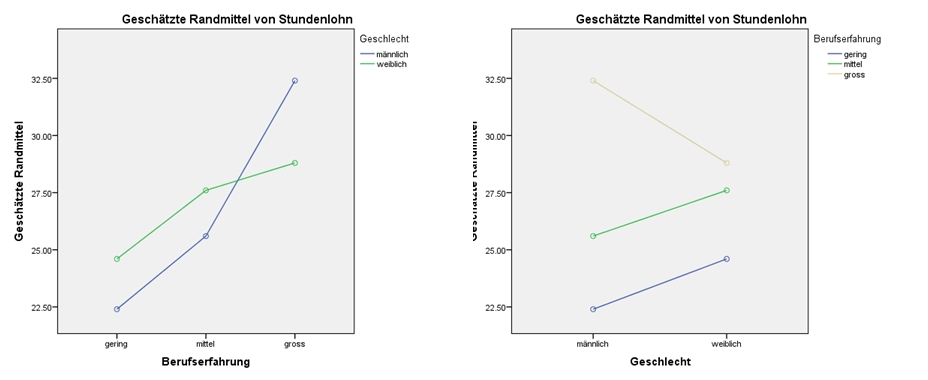
Abbildung 7: SPSS-Output – Profildiagramm für Berufserfahrung mit getrennten Linien für Geschlecht und Profildiagramm für Geschlecht mit getrennten Linien für Berufserfahrung
Das linke Profildiagramm in Abbildung 7 zeigt, dass die Berufserfahrung und der Stundenlohn zusammenhängen. Dieser Zusammenhang kann daran erkannt werden, dass die Linien beide eine ähnliche Steigung aufweisen – in diesem Fall steigt der Lohn mit der Berufserfahrung. Verliefen die Linien horizontal oder würde sich die Steigung der beiden Linien sozusagen „aufheben“, so läge vermutlich kein Haupteffekt der Berufserfahrung vor. Dass kein Effekt des Geschlechts vorliegt, wird daran ersichtlich, dass die beiden Kurven im Profildiagramm sehr nahe beieinander liegen. Eine Interaktion wird durch stark unterschiedliche Steigungen der Linien ersichtlich (also: nicht parallel verlaufende Linien). Hier zeigt sich, dass bei geringer Berufserfahrung Frauen einen höheren Lohn erhalten, während der Lohn der Männer bei hoher Erfahrung über jenem der Frauen liegt. Der Anstieg des Lohnes beim Schritt von geringer zu mittlerer Berufserfahrung scheint bei beiden Geschlechtern ähnlich gross (in absoluten Zahlen), während sich der Schritt von mittlerer zu hoher Erfahrung für Männer stark und für Frauen kaum zu lohnen scheint.
Wie dem Profildiagramm auf der rechten Seite in Abbildung 7 entnommen werden kann, zeigt sich kein Haupteffekt des Geschlechts: Die Werte des Stundenlohnes auf der linken Seite des Diagrammes („männlich“) scheinen insgesamt nicht höher zu liegen als die Werte des Stundenlohnes auf der rechten Seite („weiblich“). Den Haupteffekt der Berufserfahrung kann daran erkannt werden, dass die Kurven auseinanderliegen. Die Interaktion von Berufserfahrung und Geschlecht auf den Stundenlohn wird durch die nicht parallel verlaufenden Kurven ersichtlich. Die inhaltliche Interpretation ist dieselbe wie zum linken Profildiagramm in Abbildung 7.
3.6. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel sind zwar einige der Mittelwertsunterschiede zwar signifikant, doch es stellt sich die Frage, ob sie gross genug sind, um als bedeutend eingestuft zu werden.
Es gibt verschiedene Arten die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Der Korrelationskoeffizient eignet sich sehr gut, da die Effektstärke dabei immer zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Wenn sich jedoch die Gruppen hinsichtlich ihrer Grösse stark unterscheiden, wird empfohlen, d von Cohen zu wählen, da r durch die Grössenunterschiede verzerrt werden kann.
Da SPSS das partielle Eta-Quadrat ausgibt, wird dieses hier in die Effektstärke nach Cohen (1992) umgerechnet. In diesem Fall befindet sich die Effektstärke immer zwischen 0 und unendlich.
Um zu beurteilen, wie gross dieser Effekt ist, kann man sich an der Einteilung von Cohen (1988) orientieren:
f = .10 entspricht einem schwachen Effekt
f = .25 entspricht einem mittleren Effekt
f = .40 entspricht einem starken Effekt
Damit entsprechen die Effektstärken von 2.49 und 1.15 beide einem starken Effekt.
3.7. Eine typische Aussage
Es zeigt sich, dass das Gesamtmodell signifikant ist (F(5,24) = 36.22, p < .001, angepasstes R2 = .859, n = 30). Es zeigt sich, dass das Geschlecht alleine keinen signifikanten Zusammenhang mit der Höhe des Stundenlohnes aufweist (F(1,24) = .76, p = .678). Je nach Berufserfahrung dagegen werden unterschiedliche Löhne berichtet (F(2,24) = 74.53, p < .001, ηp2 = .861). Bonferroni-korrigierte Post-hoc-Tests zeigen, dass sich alle drei Levels der Berufserfahrung signifikant unterscheiden: tiefe Erfahrung (M = 23.5, SD = 1.51), mittlere Erfahrung (M = 26.6, SD = 1.65) und hohe Erfahrung (M = 30.6, SD = 2.37).
Zudem zeigt sich eine signifikante Interaktion von Geschlecht und Berufserfahrung auf den Lohn (F(2,24) = 15.94, p < .001, ηp2 = .571). Dies weist darauf hin, dass sich Berufserfahrung je nach Geschlecht unterschiedlich auswirkt. Bei geringer Erfahrung liegt der Lohn der Frauen (M = 24.6, SD = 1.34) über jenem der Männer (M = 22.4, SD = .55). Dies ist auch bei mittlerer Erfahrung der Fall (Frauen: M = 27.6, SD = 1.82; Männer: M = 25.6, SD = .55). Bei hoher Erfahrung ist es genau umgekehrt: Der Lohn der Männer (M = 32.4, SD = 1.52) liegt deutlich über jenem der Frauen (M = 28.8, SD = 1.48).
Die Effektstärken sind sowohl für den Haupteffekt der Berufserfahrung (f = 2.49) als auch für die Interaktion (f = 1.15) nach Cohen (1992) als stark einzustufen.