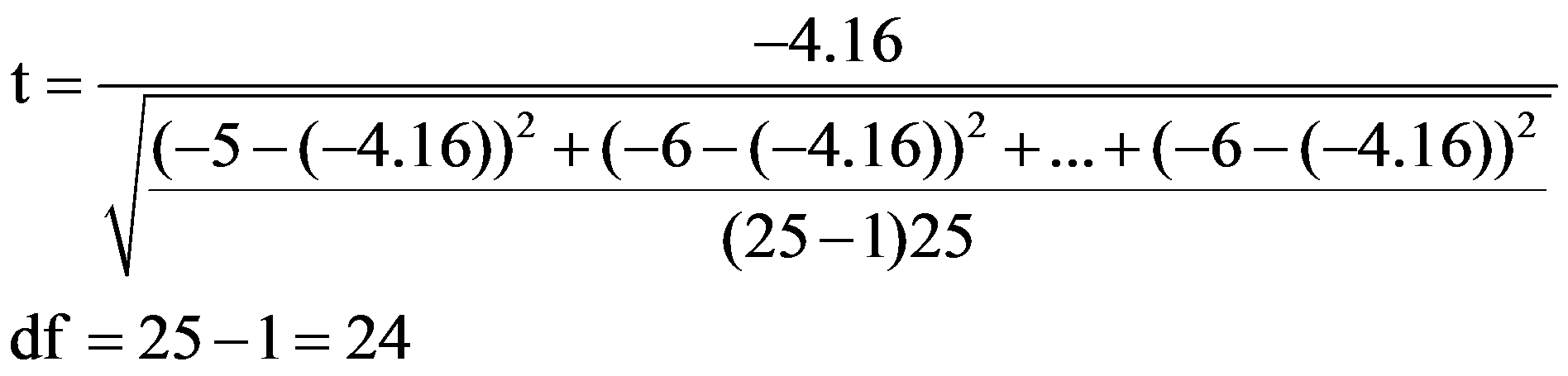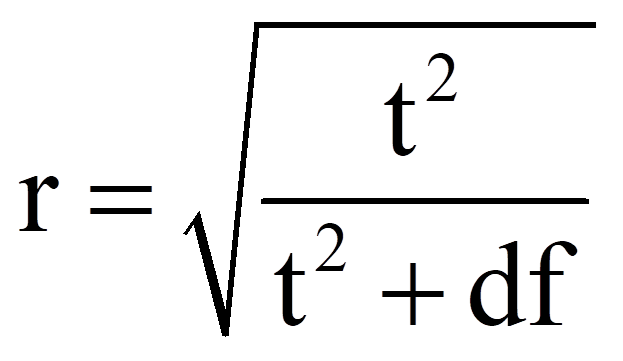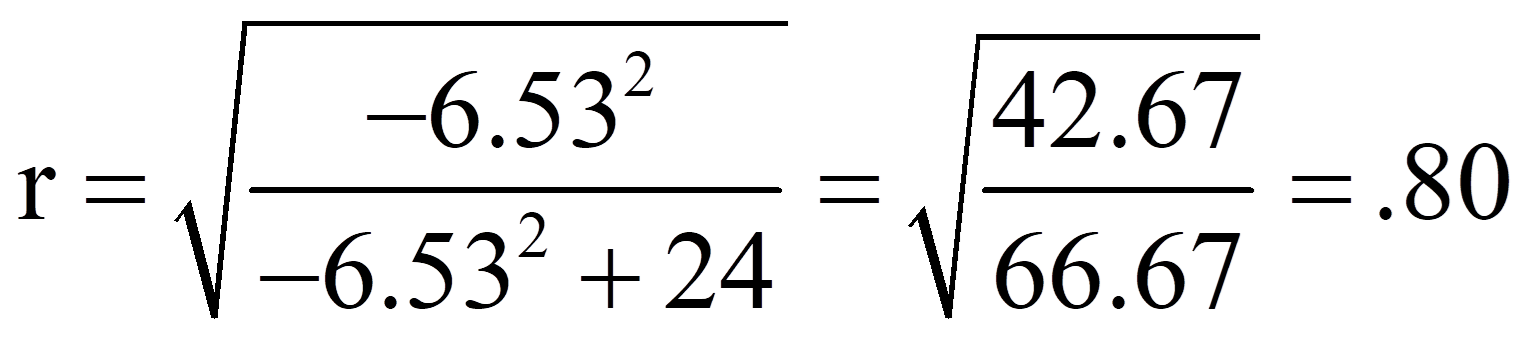 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen des t-Tests für abhängige Stichproben
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Teststatistik
3. t-Test für abhängige Stichproben mit SPSS
3.1. SPSS-Befehle
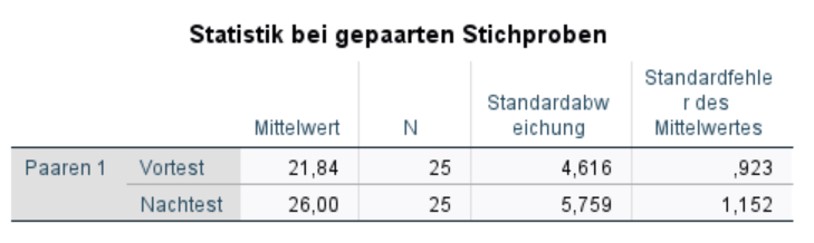
3.2. Deskriptive Statistiken und Korrelation
3.3. Ergebnisse des t-Tests für abhängige Stichproben
3.4 Berechnung der Effektstärke
3.5. Eine typische Aussage
Quick Start
| Wozu wird der t-Test für abhängige Stichproben verwendet? Der t-Test für abhängige Stichproben testet, ob die Mittelwerte zweier abhängiger Stichproben verschieden sind. SPSS-Menü
Analysieren > Analysieren > Mittelwerte vergleichen > t-Test bei verbundenen Stichproben SPSS-Syntax
T-TEST PAIRS =Variable1 WITH Variable2 (PAIRED) /CRITERIA=CI (.95) /MISSING=ANALYSIS. SPSS-Beispieldatensatz
t-Test_abhaengig |
1. Einführung
Der t-Test für abhängige Stichproben testet, ob die Mittelwerte zweier abhängiger Stichproben verschieden sind.
Von „abhängigen Stichproben“ respektive „verbundenen Stichproben“ wird gesprochen, wenn ein Messwert in einer Stichprobe und ein bestimmter Messwert in einer anderen Stichprobe sich gegenseitig beeinflussen. In drei Situationen ist dies der Fall:
- Messwiederholung: Die Messwerte stammen von der gleichen Person, zum Beispiel bei einer Messung vor und nach einem Treatment oder wenn verschiedene Treatments auf die gleiche Person angewandt werden und verglichen werden sollen.
- Natürliche Paare: Die Messwerte stammen von verschiedenen Personen, diese gehören aber zusammen (z.B.: Ehefrau – Ehemann, Psychologe – Patient, Anwalt – Klient, Eigentümer – Mieter oder Zwillinge).
- Matching: Die Messwerte stammen von verschiedenen Personen, die einander zugeordnet wurden, zum Beispiel aufgrund eines vergleichbaren Werts auf einer Drittvariablen (die nicht im Zentrum der Untersuchung steht).
Die Fragestellung des t-Tests für abhängige Stichproben wird oft so verkürzt: „Unterscheiden sich die Mittelwerte von zwei abhängigen Stichproben?“
1.1. Beispiele für mögliche Fragestellungen
- Schätzen Ehepartner ihre Konfliktlösefähigkeiten unterschiedlich ein?
- Reagieren Zwillinge unterschiedlich auf einen Werbespot?
- Gibt es Unterschiede zwischen den Testwerten von Probanden vor und nach einem Gedächtnistraining?
1.2. Voraussetzungen des t-Tests für abhängige Stichproben
| ✓ | Die abhängige Variable ist intervallskaliert |
| ✓ | Es liegen zwei verbundene Stichproben oder Gruppen vor, aber die verschiedenen Messwertpaare sind voneinander unabhängig (e.g. Paar A und Paar B sind voneinander unabhängig) |
| ✓ | Die Unterschiede zwischen den verbundenen Testwerten sind in der Grundgesamtheit normalverteilt (bei Stichproben > 30 sind Verletzungen unproblematisch) |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
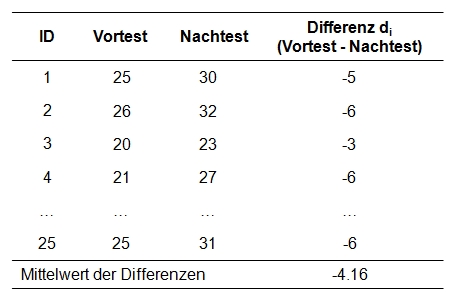
Eine Experimentalgruppe von 25 Senioren hat an einem 8-wöchigen Gedächtnistraining teilgenommen. Die Gedächtnisleistung wird zu zwei Zeitpunkten gemessen: vor dem Training (Vortest) und nach dem Training (Nachtest). Es soll geprüft werden, ob das Gedächtnistraining gewirkt hat. Können sich die Probanden nach dem Training mehr Wörter einer Liste von insgesamt 40 Wörtern merken?
Der zu analysierende Datensatz enthält neben einer Probandennummer (ID) die beiden Messungen (Gedächtnis_Vortest, Gedächtnis_Nachtest).
-
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
Berechnen der Teststatistik
Bereits „von Auge“ zeigt sich ein Unterschied zwischen den Mittelwerten (siehe Abbildung 1). Um zu überprüfen, ob dieser Unterschied statistisch signifikant ist, muss die dazugehörige Teststatistik berechnet werden. Die Verteilung der Teststatistik t folgt einer theoretischen t-Verteilung, deren Form sich in Abhängigkeit der Freiheitsgrade unterscheidet. Die dem Test zu Grunde liegende t-Verteilung gibt dem Test den Namen t-Test.
Die Teststatistik t berechnet sich wie folgt:
Signifikanz der Teststatistik
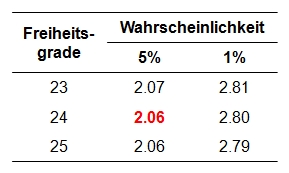
Der berechnete Wert muss nun auf Signifikanz geprüft werden. Dazu wird die Teststatistik mit dem kritischen Wert der durch die Freiheitsgrade bestimmten t-Verteilung verglichen. Dieser kritische Wert kann Tabellen entnommen werden. Abbildung 2 zeigt einen Ausschnitt einer t-Tabelle, der einige kritische Werte für die Signifikanzniveaus .05 und .01 zeigt.
-
Für das vorliegende Beispiel beträgt der kritische Wert 2.06 bei df = 24 und α = .05 (siehe Ab-bildung 2). Ist der Betrag der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel der Fall (|-6.53| > 2.06). Es kann also davon ausgegangen werden, dass sich die beiden Mittelwerte unterscheiden (t = -6.53, p < .001, n = 25).
3. t-Test für abhängige Stichproben mit SPSS
3.1. SPSS-Befehle
SPSS-Syntax
T-TEST PAIRS=Gedächtnis_Vortest WITH Gedächtnis_Nachtest (PAIRED)
/CRITERIA=CI (.95)
/MISSING=ANALYSIS.
In Abbildung 4 zeigt sich, dass sich die Mittelwerte augenscheinlich etwas unterscheiden. Diese Tabelle wird später für die Berichterstattung verwendet.
Bei Messwiederholungen ist es möglich, dass die Daten der ersten und zweiten Erhebung (respektive eines Messwertpaars) miteinander korrelieren. Es ist plausibel, dass zwei verbundene Messungen sich ähnlich sind und dass innerhalb eines Messwertpaares eher geringere Unterschiede auftreten als zwischen den Paaren. Im SPSS-Output wird daher eine Pearson Korrelation der beiden Messzeitpunkte ausgegeben (siehe Abbildung 5). Für das Beispiel ergibt sich eine sehr hohe Korrelation
(r = .834, p < .001, n = 25).
3.3. Ergebnisse des t-Tests für abhängige Stichproben
Die Teststatistik beträgt t = -6.532 und der zugehörige Signifikanzwert p < .001. Damit ist der Unterschied signifikant: Die Mittelwerte der beiden Messzeitpunkte (Vortest und Nachtest) unterscheiden sich (t = -6.532, p < .001, n = 25).
3.4 Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel ist der Mittelwertsunterschied zwar signifikant, doch es stellt sich die Frage, ob der Unterschied gross genug ist, um ihn als bedeutend einzustufen.
Es gibt verschiedene Arten die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Der Korrelationskoeffizient eignet sich sehr gut, da die Effektstärke dabei immer zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Wenn sich jedoch die Gruppen hinsichtlich ihrer Grösse stark unterscheiden, wird empfohlen, d von Cohen zu wählen, da r durch die Grössenunterschiede verzerrt werden kann.
Zur Berechnung des Korrelationskoeffizienten r werden der t-Wert und die Freiheitsgrade (df) verwendet, die Abbildung 6 entnommen werden können:
3.5. Eine typische Aussage
Es zeigt sich, dass das Gedächtnistraining einen statistisch signifikanten Einfluss auf die Leistung im Gedächtnistest hat (t = -6.532, p < .001, n = 25). Nach dem Gedächtnistraining (M = 26.00, SD = 5.76) schneiden die Probanden signifikant besser ab als vor dem Gedächtnistraining (M = 21.84, SD = 4.62). Die Effektstärke nach Cohen (1992) liegt bei r = .80 und entspricht damit einem starken Effekt.