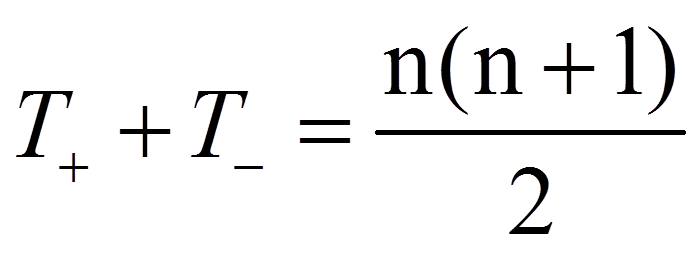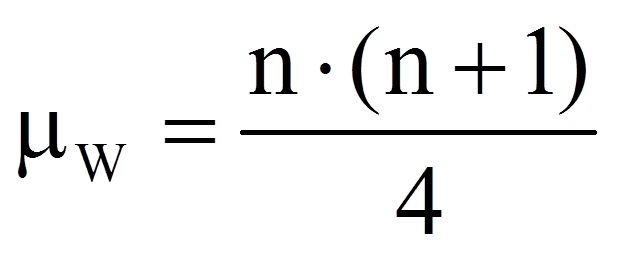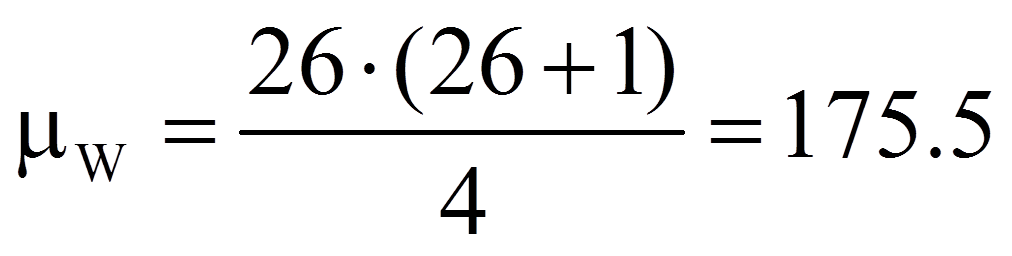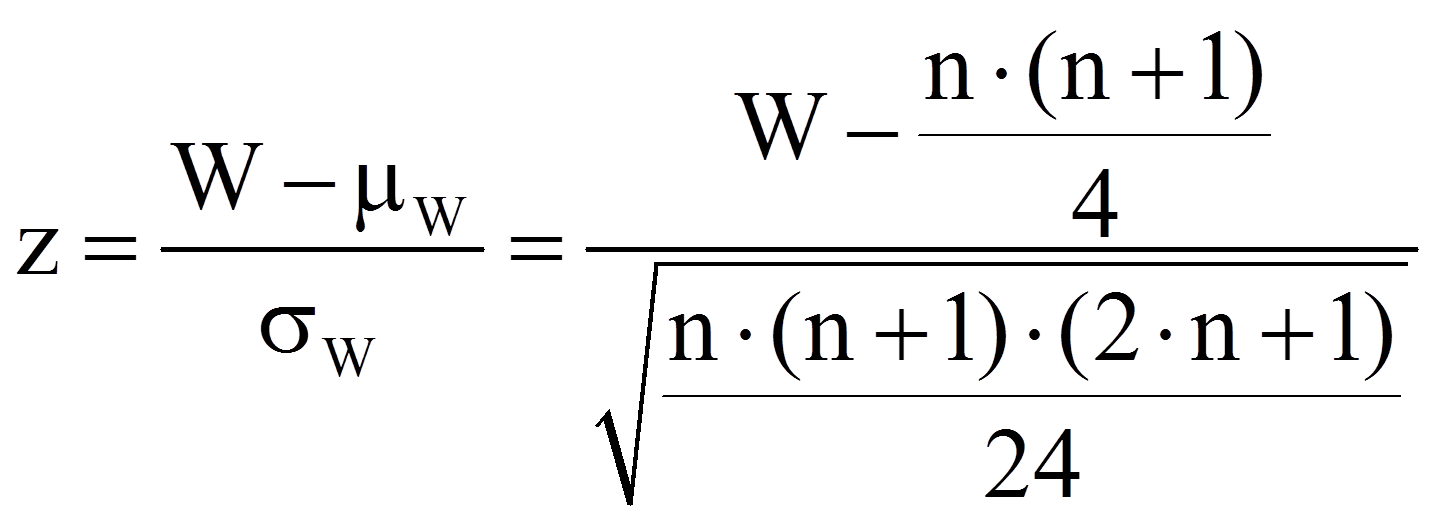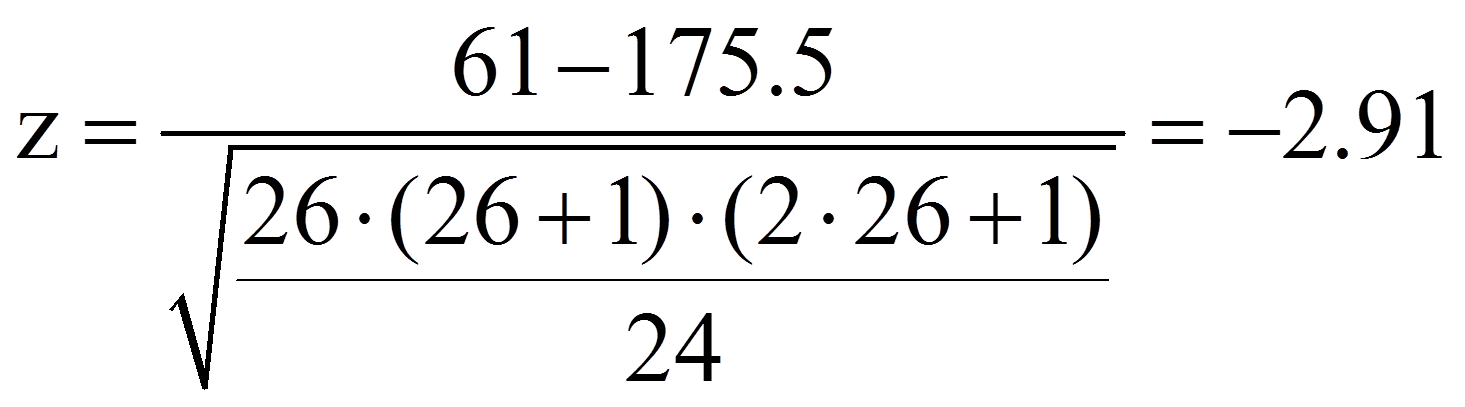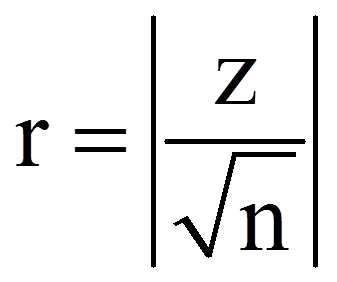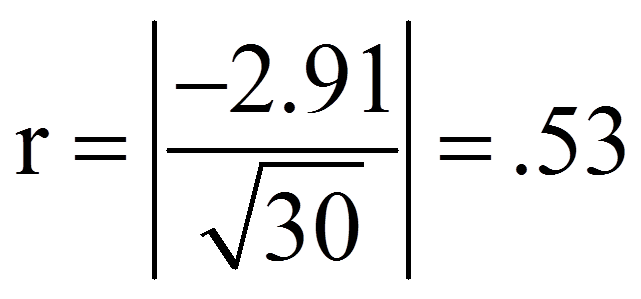Wilcoxon-Vorzeichen-Rang-Test

Der Wilcoxon-Test – auch Wilcoxon-Vorzeichen-Rang-Test genannt (engl. „Wilcoxon signed-rank test“, kurz WSR) – für abhängige Stichproben testet, ob die zentralen Tendenzen zweier abhängiger Stichproben verschieden sind. Der Wilcoxon-Test wird verwendet, wenn die Voraussetzungen für einen t-Test für abhängige Stichproben nicht erfüllt sind.

Von „abhängigen Stichproben“ wird gesprochen, wenn ein Messwert in einer Stichprobe und ein bestimmter Messwert in einer anderen Stichprobe sich gegenseitig beeinflussen. In drei Situationen ist dies der Fall:

• Messwiederholung: Die Messwerte stammen von der gleichen Person, zum Beispiel bei einer Messung vor einem Treatment und nach einem Treatment oder wenn verschiedene Treatments auf die gleiche Person angewendet werden und verglichen werden sollen.
• Natürliche Paare: Die Messwerte stammen von verschiedenen Personen, welche irgendwie zusammengehören (z.B.: Ehefrau – Ehemann, Psychologe – Patient, Anwalt – Klient, Eigentümer – Mieter oder Zwillinge).
• Matching: Die Messwerte stammen von verschiedenen Personen, die einander zugeordnet wurden, zum Beispiel aufgrund eines vergleichbaren Werts auf einer Drittvariablen (die nicht im Zentrum der Untersuchung steht).

Der Wilcoxon-Test ist das nichtparametrische Äquivalent des t-Tests für abhängige Stichproben und wird angewandt, wenn die Voraussetzungen für ein parametrisches Verfahren nicht erfüllt sind. Nicht-parametrische Verfahren sind auch bekannt als „voraussetzungsfreie Verfahren“, weil sie geringere Anforderungen an die Verteilung der Messwerte in der Grundgesamtheit stellen. So müssen die Daten nicht normalverteilt sein und die abhängige Variable muss lediglich ordinalskaliert sein. Auch bei kleinen Stichproben und Ausreissern kann ein Wilcoxon-Test berechnet werden.

Alternativ zum Wilcoxon-Test kann auch der Vorzeichentest ausgeführt werden. Der Vorzeichentest berechnet für alle Fälle die Differenzen zwischen den beiden Variablen und klassifiziert sie als positiv, negativ oder verbunden. Falls die beiden Variablen ähnlich verteilt sind, unterscheidet sich die Zahl der positiven und negativen Differenzen nicht signifikant. Der Wilcoxon-Test berücksichtigt sowohl Informationen über die Vorzeichen der Differenzen als auch die Grösse der Differenzen zwischen den Paaren. Da der Wilcoxon-Test mehr Informationen über die Daten aufnimmt, kann er mehr leisten als der Vorzeichentest.

Die Fragestellung des Wilcoxon-Tests für abhängige Stichproben wird oft so verkürzt:
„Unterscheiden sich die zentralen Tendenzen zweier abhängiger Stichproben?“

• Verkauft sich ein Produkt nach der Vergabe eines Rabatts bei Onlinekauf besser als zuvor?
• Unterscheiden sich Ehepaare in ihrer Kreditkartennutzung?
• Erreichen Tennisspieler nach einem Trainingscamp eine höhere ATP-Rangierung als vorher?
• Zeigen Alzheimer-Patienten auf einer Emotionsskala nach einem Besuch von Verwandten andere Werte als vor deren Besuch?

In 30 Geschäftsstellen wurde die Anzahl täglicher Verkäufe eines Produktes vor und nach der Vergabe eines Rabattes erhoben. Es soll geprüft werden, ob es Unterschiede hinsichtlich der zentralen Tendenz der Anzahl täglicher Verkäufe vor und nach dem Rabatt gibt, also ob der Rabatt einen Einfluss auf die Verkaufszahlen hat. Eine Voruntersuchung hat gezeigt, dass die Daten die Voraussetzungen für einen t-Test für abhängige Stichproben nicht erfüllen.

Der zu analysierende Datensatz enthält neben einer Identifikationsnummer der Geschäftsstelle (ID) die beiden Messungen der Verkaufszahlen (Vorher für die Erhebung vor der Einführung des Rabatts, Nachher für die Erhebung nach dem Vergeben des Rabatts).

Abbildung 1: Beispieldaten und erste Berechnungsschritte

Der Datensatz kann unter Quick Start heruntergeladen werden.

Berechnen der Teststatistik

Der Wilcoxon-Test basiert auf der Idee der Rangierung der Daten. Das heisst, es wird nicht mit den Differenzen der Messwerte selbst gerechnet, sondern diese werden durch Ränge ersetzt, mit welchen der eigentliche Test durchgeführt wird. Damit beruht die Berechnung des Tests ausschliesslich auf der Ordnung der Differenzen (grösser als, kleiner als). Die absoluten Abstände zwischen den Differenzen werden nicht berücksichtigt.

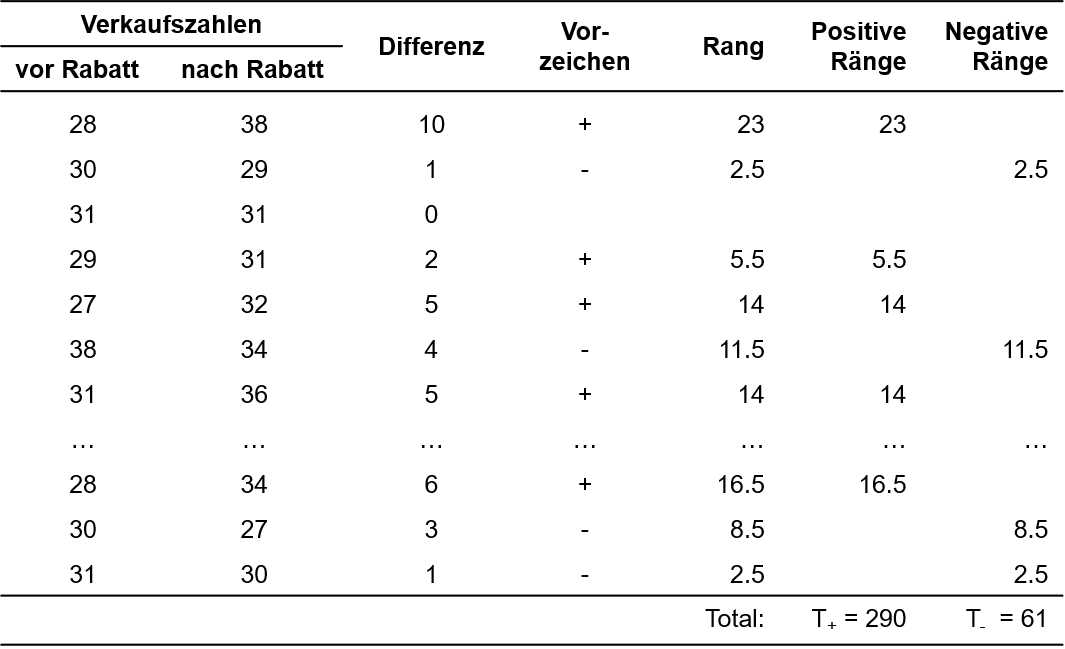
Zunächst wird für jedes Messwertpaar die Differenz der beiden Messungen berechnet (Nachher – Vorher) und es werden sowohl der Betrag der Differenz (siehe Spalte „Differenz“ in Abbildung 1) als auch das Vorzeichen der Differenz notiert (Spalte „Vorzeichen“).

Diese absoluten Differenzen werden mit Rängen versehen. Beträgt die Differenz eines Datenpaares 0, so wird dieses Paar von der Rangierung ausgeschlossen. Es wird unabhängig vom Vorzeichen mit der kleinsten Differenz begonnen und aufwärts nummeriert. Kommt ein Messwert mehrfach vor (engl. „ties“), so werden sogenannte „verbundene Ränge“ gebildet. Wenn beispielsweise Rang 5 und 6 beide die gleichen Messwerte aufweisen, wird aus diesen beiden der Mittelwert gebildet ((5 + 6)/2 = 5.5) und die Ränge 5 und 6 werden neu beide mit dem Rang 5.5 versehen. Im Beispiel ist die Differenz 1 der kleinste Wert und kommt insgesamt viermal vor. Das entspricht den potenziellen Rängen 1 bis 4. Nun wird der Durchschnitt dieser Ränge ((1+2+3+4)/4 = 2.5) berechnet. Der Differenzwert 1 erhält somit den Rang 2.5 (siehe Spalte „Rang“).

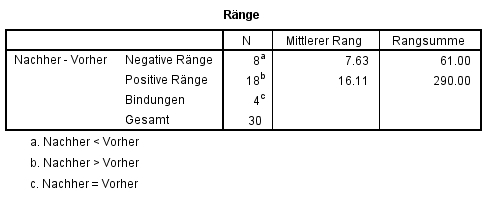
Ist allen Paardifferenzen ein Rang zugeordnet, so werden die positiven und die negativen Rangplätze separat notiert (Spalten „Positive Ränge“; „Negative Ränge“) und aufsummiert (Zeile „Total“).

Zwischen diesen Rangsummen besteht der folgende Zusammenhang:

mit

Als Teststatistik W wird nun der kleinere der beiden Werte verwendet:

Für das Beispiel ist dies (siehe Rangsummen in Abbildung 1):

Je geringer die Unterschiede der zentralen Tendenzen sind, desto näher liegt der Wert der Teststatistik bei dem Wert, der sich ergibt, wenn es keine Unterschiede gäbe (der Erwartungswert für die Rangsummen unter Gültigkeit der Nullhypothese). Dieser Wert errechnet sich als Hälfte der Summe der beiden Rangsummen:

mit

Für das Beispiel sind 26 der 30 Paardifferenzen ≠ 0. Also ergibt dies:

Signifikanz der Teststatistik

Der berechnete Wert muss nun auf Signifikanz geprüft werden. Dazu wird die Teststatistik mit einem kritischen Wert verglichen. Ist die Stichprobe hinreichend gross (n > 20), so ist der kritische Wert asymptotisch normalverteilt und die Signifikanz kann geprüft werden, indem der eben berechnete W-Wert wie folgt z-standardisiert wird:

mit

Da für das Beispiel die Stichprobengrösse hinreichend gross ist (n = 30), wird ein z-Wert berechnet:

Dieser z-Wert kann nun auf Signifikanz geprüft werden, indem er mit dem kritischen Wert der Standardnormalverteilung (z-Verteilung) verglichen wird. Dieser kritische Wert kann Tabellen entnommen werden. Für das zweiseitige Signifikanzniveau .05 beträgt er ±1.96. Ist der Betrag der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel der Fall (|-2.91| > 1.96). Es kann also davon ausgegangen werden, dass sich die zentralen Tendenzen unterscheiden (Asymptotischer Wilcoxon-Test: z = -2.91, p = .004, n = 30).

Ist die Stichprobe nicht hinreichend gross, so muss der kritische W-Wert in einer Tabelle nachgeschlagen werden. In SPSS wird zur Beurteilung in diesem Fall die exakte Signifikanz verwendet.

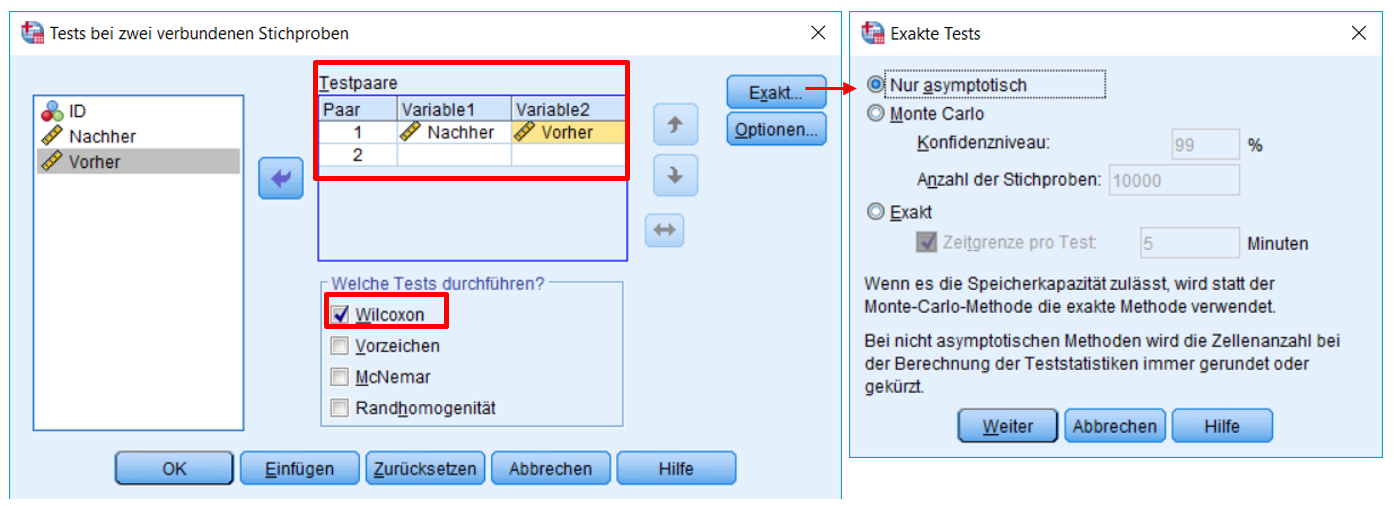
SPSS-Menü: Analysieren > Nichtparametrische Tests > Klassische Dialogfelder > Zwei verbundene Stichproben

Abbildung 2: Klicksequenz in SPSS

Hinweis

• Bei n > 30 kann Nur asymptotisch verwendet werden. Ist die Stichprobe jedoch klein, so empfiehlt sich die Einstellung Exakt.

SPSS-Syntax

NPAR TESTS
/WILCOXON = Vorher WITH Nachher (PAIRED)
/PMISSING = ANALYSIS.

In Abbildung 3 lässt die Spalte „Mittlerer Rang“ bereits vermuten, dass die beiden Stichproben eine unterschiedliche zentrale Tendenz aufweisen.

Abbildung 4: SPSS-Output – Teststatistik

Die Teststatistik beträgt z = -2.912 und der zugehörige Signifikanzwert p = .004 (siehe Abbildung 4). Damit ist der Unterschied signifikant: Die zentralen Tendenzen der beiden Messzeitpunkte unterscheiden sich (Asymptotischer Wilcoxon-Test: z = -2.91, p = .004, n = 30).

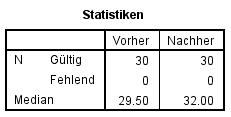
Über das SPSS-Menü Analysieren > Deskriptive Statistiken > Häufigkeiten (Statistiken: Median) werden die Mediane ausgegeben.

SPSS-Syntax

FREQUENCIES VARIABLES=Vorher Nachher
/FORMAT=NOTABLE
/STATISTICS=MEDIAN
/ORDER=ANALYSIS.

Dies führt zum folgenden SPSS-Output (Abbildung 5), der die beiden Mediane angibt:

Abbildung 5: SPSS-Output – Deskriptive Statistiken der beiden Messzeitpunkte

Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel sind zwar einige der Mittelwertsunterschiede zwar signifikant, doch es stellt sich die Frage, ob sie gross genug sind, um als bedeutend eingestuft zu werden.

Es gibt verschiedene Arten, die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Der Korrelationskoeffizient eignet sich sehr gut, da die Effektstärke dabei immer zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Wenn sich jedoch die Gruppen hinsichtlich ihrer Grösse stark unterscheiden, wird empfohlen, d von Cohen zu wählen, da r durch die Grössenunterschiede verzerrt werden kann.

Zur Berechnung des Korrelationskoeffizienten r werden der z-Wert und die Stichprobengrösse (n) verwendet, die dem SPSS-Output (Abbildungen 3 und 4) entnommen werden können:

Für das obige Beispiel ergibt das folgende Effektstärke r:

Zur Beurteilung der Grösse des Effektes dient die Einteilung von Cohen (1992):

r = .10 entspricht einem schwachen Effekt
r = .25 entspricht einem mittleren Effekt
r = .40 entspricht einem starken Effekt

Damit entspricht die Effektstärke von .53 einem starken Effekt.

Die Verkaufszahlen sind nach der Gewährung eines Rabattes signifikant höher (Mdn = 32.00) als davor (Mdn = 29.50; asymptotischer Wilcoxon-Test: z = -2.91, p = .004, n = 30). Die Effektstärke liegt bei r = .53 und entspricht nach Cohen (1992) einem starken Effekt.

top