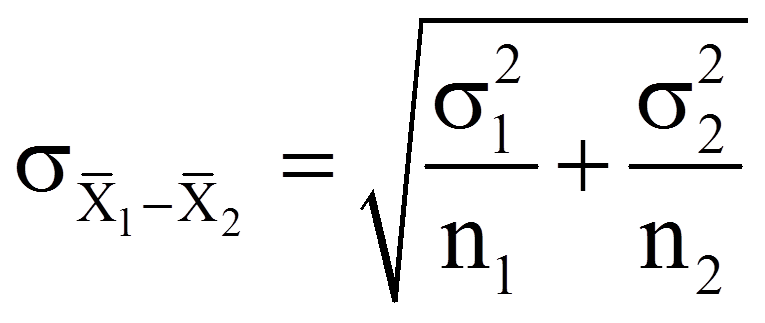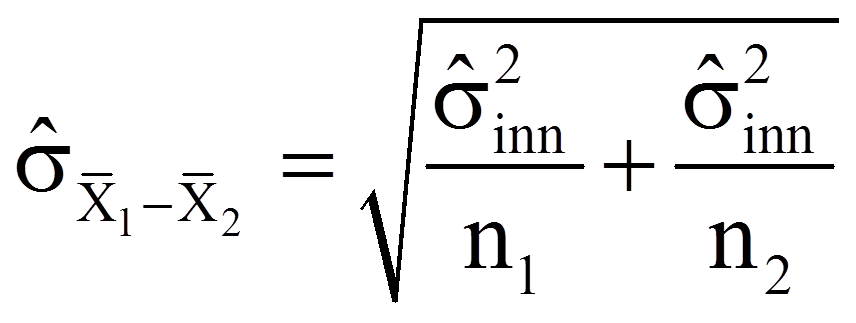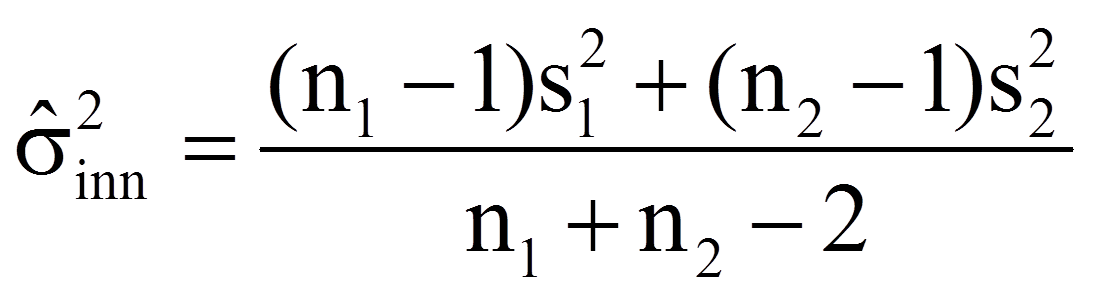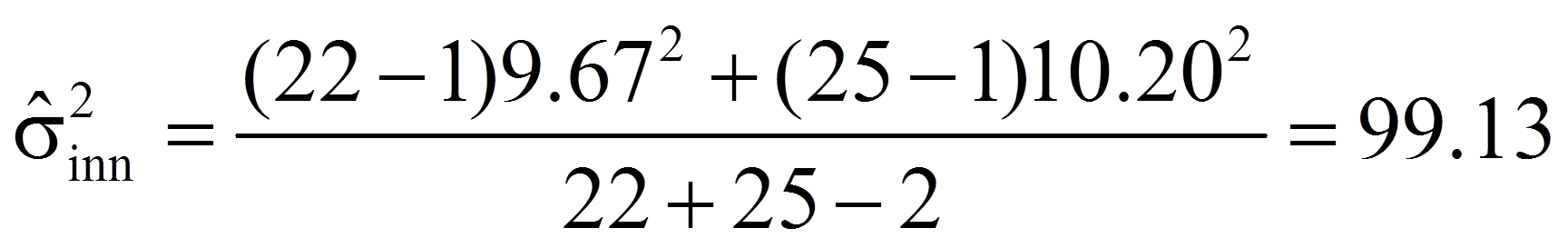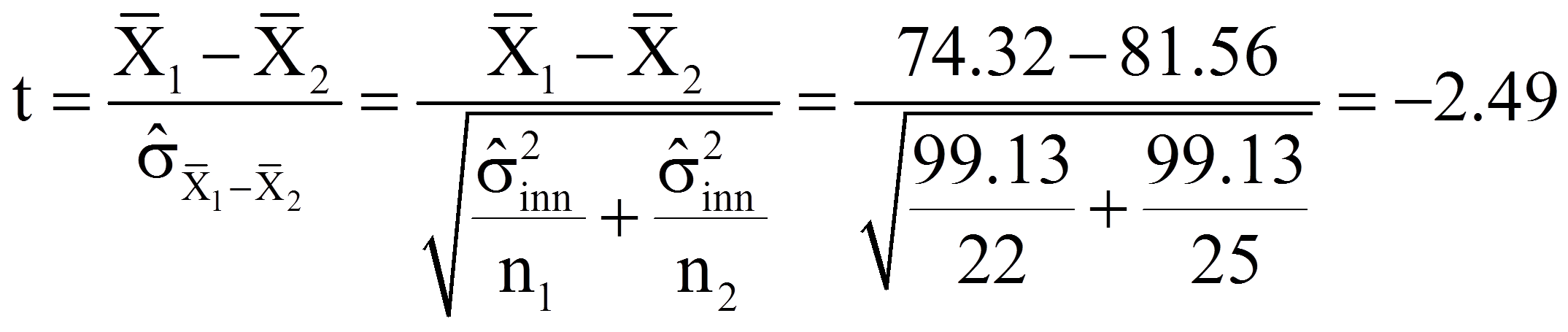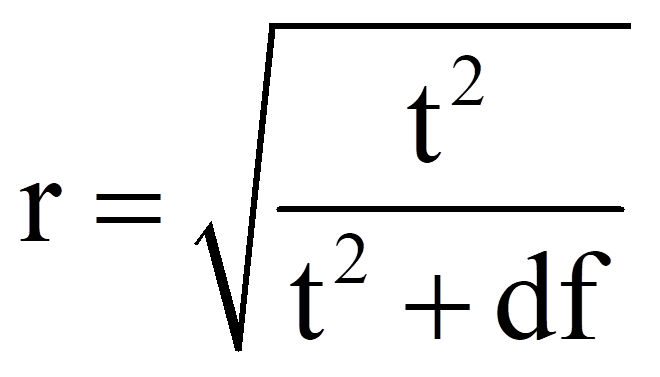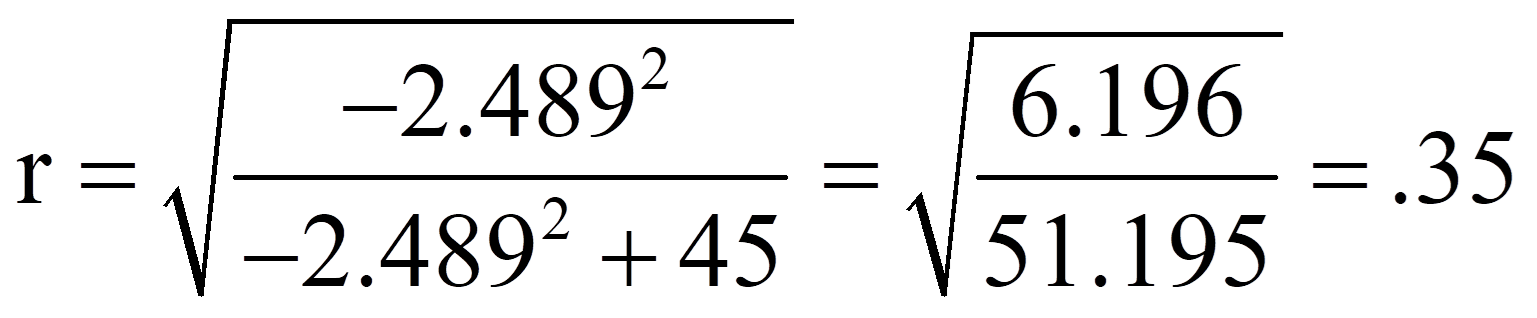Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen des t-Tests für unabhängige Stichproben
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Teststatistik
3. t-Test für unabhängige Stichproben mit SPSS
3.1. SPSS-Befehle
3.2. Deskriptive Statistiken
3.3. Test auf Varianzhomogenität (Levene-Test)
3.4. Ergebnisse des t-Tests für unabhängige Stichproben
3.5. Berechnung der Effektstärke
3.6. Eine typische Aussage
Quick Start
| Wozu wird der t-Test für unabhängige Stichproben verwendet? Der t-Test für unabhängige Stichproben testet, ob die Mittelwerte zweier unabhängiger Stichproben verschieden sind. SPSS-Menü
Analysieren > Mittelwerte vergleichen > t-Test bei unabhängigen Stichproben SPSS-Syntax
T-TEST GROUPS=unabhängige Variable (1 2) /MISSING=ANALYSIS /VARIABLES=abhängige Variable /CRITERIA=CI (.95). SPSS-Beispieldatensatz:
t-Test_unabhaengig |
1. Einführung
Der t-Test für unabhängige Stichproben testet, ob die Mittelwerte zweier unabhängiger Stichproben verschieden sind.
Die Fragestellung des t-Tests für unabhängige Stichproben wird oft so verkürzt:
„Unterscheiden sich die Mittelwerte zweier unabhängiger Stichproben?“
1.1. Beispiele für mögliche Fragestellungen
- Sinkt die Verkehrsbelastung (Anzahl Fahrzeuge pro Stunde) in der Hauptverkehrszeit in einem Dorf nach dem Bau einer Umfahrungsstrasse?
- Unterscheiden sich Personen mit selbstständiger oder unselbständiger Tätigkeit bezüglich ihrer Zufriedenheit mit ihrer beruflichen Situation?
- Gibt es einen Unterschied in der durchschnittlichen Anzahl Einbrüche in Häuser mit und ohne Alarmanlage?
- Hat das Hören von klassischer Musik oder Schlagermusik während des Lernens von Vokabeln einen unterschiedlichen Einfluss auf den Lernerfolg?
1.2. Voraussetzungen des t-Tests für unabhängige Stichproben
| ✓ | Die abhängige Variable ist intervallskaliert |
| ✓ | Es liegt eine unabhängige Variable vor, mittels der die beiden zu vergleichenden Gruppen gebildet werden |
| ✓ | Das untersuchte Merkmal ist in den Grundgesamtheiten der beiden Gruppen normalverteilt |
| ✓ | Homogenität der Varianzen: Die Gruppen kommen aus Grundgesamtheiten mit annähernd identischer Varianz (siehe Levene-Test) |
| ✓ | Die einzelnen Messwerte sind voneinander unabhängig (das Verhalten einer Versuchsperson hat keinen Einfluss auf das Verhalten einer anderen) |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
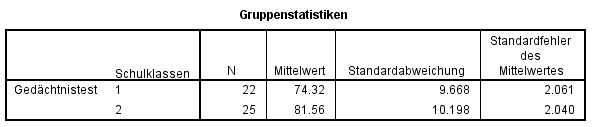
Die Schulklasse B hat ein Gedächtnistraining erhalten, die Schulklasse A nicht. Anhand eines Gedächtnistests (Index von 1 bis 100) wird nun gemessen, ob sich die beiden Gruppen in ihren Gedächtnistestresultaten unterscheiden.
Der zu analysierende Datensatz enthält neben einer Personennummer (ID) die Klassenzugehörigkeit (Schulkasse) und das Ergebnis des Gedächtnistests (Gedächtnistest).
Der Beispieldatensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
Der t-Test für unabhängige Gruppen setzt Varianzhomogenität voraus. Dies wird in Kapitel 3.3 mit SPSS geprüft. Für die manuelle Berechnung der Teststatistik wird dies einfachheitshalber nicht geprüft.
Berechnen der Teststatistik
Bereits „von Auge“ zeigt sich ein Unterschied zwischen den Mittelwerten (siehe Abbildung 1). Um zu überprüfen, ob dieser Unterschied statistisch signifikant ist, muss die dazugehörige Teststatistik berechnet werden. Die Verteilung der Teststatistik t folgt einer theoretischen t-Verteilung, deren Form sich in Abhängigkeit der Freiheitsgrade unterscheidet. Die dem Test zu Grunde liegende t-Verteilung gibt dem Test den Namen t-Test.
Die Teststatistik t berechnet sich wie folgt:
mit
mit
mit
| = | Schätzer für den Standardfehler der Verteilung der Mittelwertsdifferenzen | |
| = | Stichprobengrössen der beiden Stichproben | |
| = | Schätzer für die gepoolte Varianz der beiden Grundgesamtheiten |
Der Schätzer für die gepoolte Varianz wiederum errechnet sich wie folgt:
mit
| = | Stichprobengrössen der beiden Stichproben | |
| = | Freiheitsgrade | |
| = | Stichprobenvarianzen der Variablen x1 und x2 |
Für das vorliegende Beispiel sind die Populationsvarianzen nicht bekannt, so dass sich nach Einfügen der Werte aus Abbildung 1 in die entsprechenden Formeln folgendes ergibt:
Signifikanz der Teststatistik
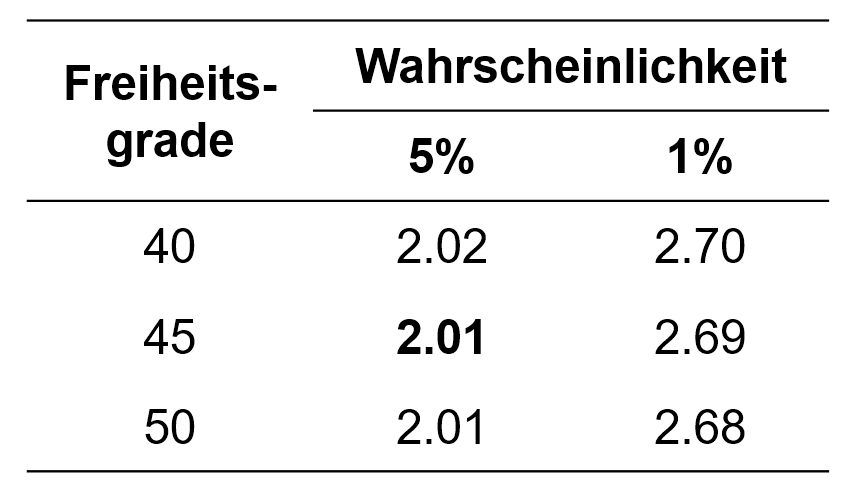
Der berechnete Wert muss nun auf Signifikanz geprüft werden. Dazu wird die Teststatistik mit dem kritischen Wert der durch die Freiheitsgrade bestimmten t-Verteilung verglichen. Dieser kritische Wert kann Tabellen entnommen werden. Abbildung 2 zeigt einen Ausschnitt einer t-Tabelle, der einige kritische Werte für die Signifikanzniveaus .05 und .01 zeigt.
Für das vorliegende Beispiel beträgt der kritische Wert 2.01 bei df = 45 und α = .05 (siehe Abbildung 2). Ist der Betrag der Teststatistik grösser als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel der Fall (|-2.49| > 2.01). Es kann also davon ausgegangen werden, dass sich die beiden Mittelwerte signifikant unterscheiden (t(45) = -2.49, p < .05).
3. t-Test für unabhängige Stichproben mit SPSS
3.1. SPSS-Befehle
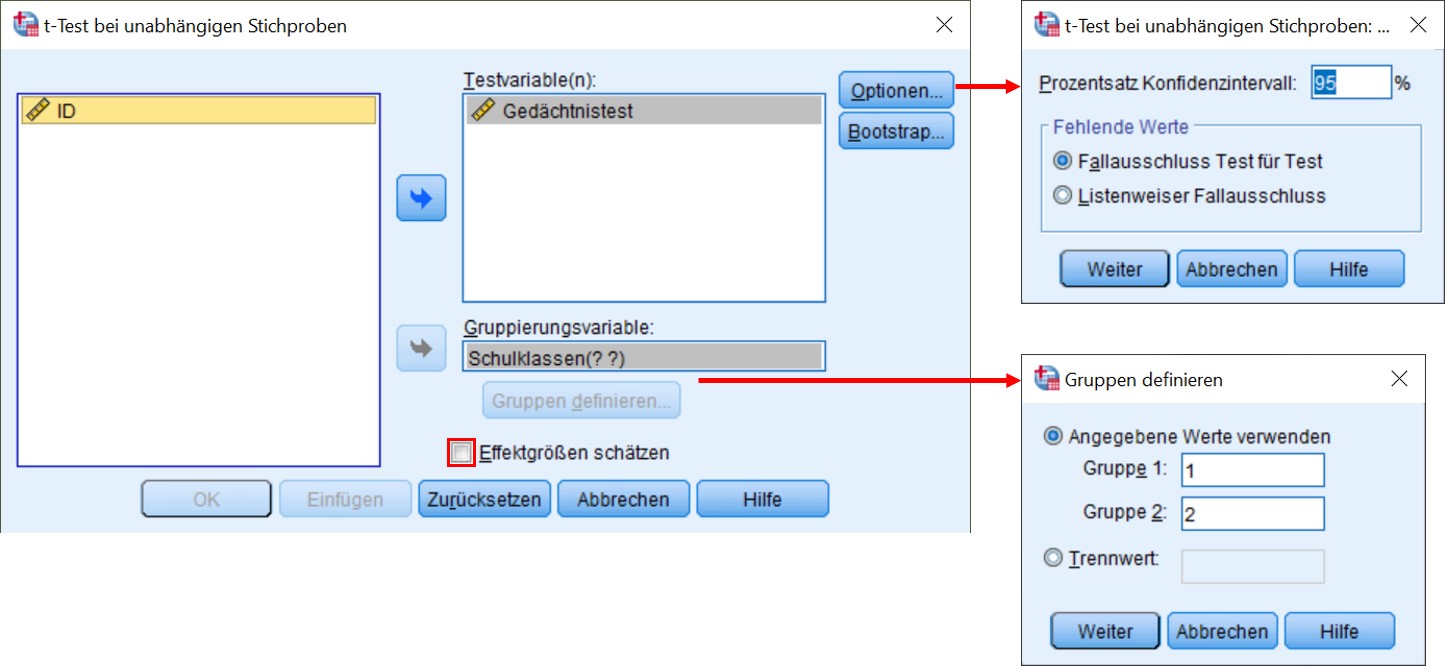
SPSS-Menü: Analysieren > Mittelwerte vergleichen > t-Test bei unabhängigen Stichproben
Hinweis
- Da die unabhängige Variable (Gruppenvariable) mehr als zwei Gruppen unterscheiden könnte, müssen unter Gruppen definieren jene Werte angegeben werden, die die beiden Gruppen beschreiben. Im Beispiel sind das 1 und 2, da im Datensatz Schulklasse A als 1 und Schulklasse B als 2 codiert wurde.
SPSS-Syntax
T-TEST GROUPS=Schulklassen (1 2)
/MISSING=ANALYSIS
/VARIABLES=Gedächtnistest
/CRITERIA=CI (.95).
3.2. Deskriptive Statistiken
In Abbildung 4 zeigt sich, dass sich die Mittelwerte augenscheinlich etwas unterscheiden. Diese Tabelle wird später für die Berichterstattung verwendet.
3.3. Test auf Varianzhomogenität (Levene-Test)
Der t-Test für unabhängige Gruppen setzt Varianzhomogenität voraus. Liegt Varianzheterogenität vor (also unterschiedliche Varianzen), so müssen unter anderem die Freiheitsgerade des t-Wertes angepasst werden. Ob die Varianzen homogen („gleich“) sind, lässt sich mit dem Levene-Test auf Varianzhomogenität prüfen. Dieser Test ist eine Variante des F-Tests.
Der Levene-Test verwendet die Nullhypothese, dass sich die beiden Varianzen nicht unterscheiden. Daher bedeutet ein nicht signifikantes Ergebnis, dass sich die Varianzen nicht unterscheiden und somit Varianzhomogenität vorliegt. Ist der Test signifikant, so wird von Varianzheterogenität ausgegangen.
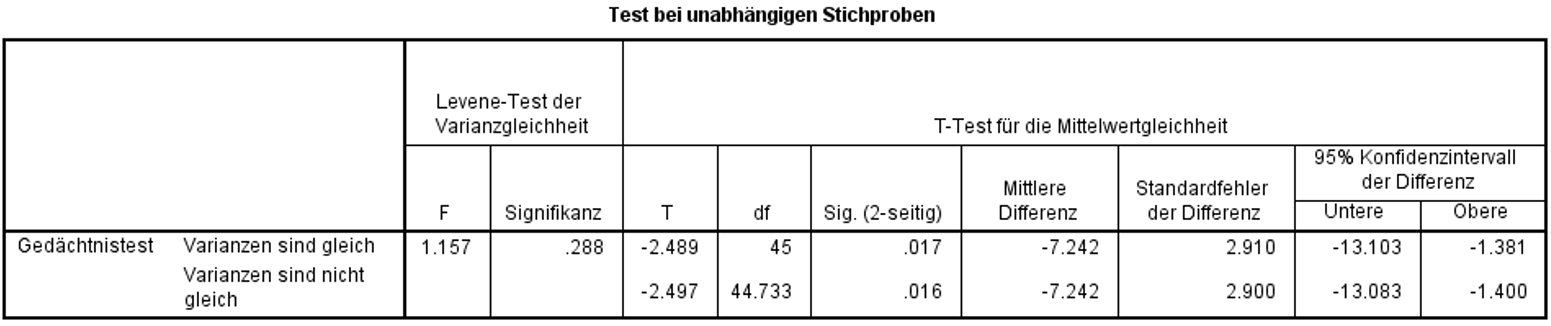
Für das Beispiel gibt SPSS einen F-Wert von 1.157 und eine dazugehörige Signifikanz von p = .288 aus (siehe Abbildung 5). Im Beispiel liegt also Varianzhomogenität vor (Levene-Test: F(1,45) = 1.157, p = .288, n = 47).
3.4. Ergebnisse des t-Tests für unabhängige Stichproben
SPSS (Abbildung 5) gibt bei der Durchführung eines t-Tests für unabhängige Stichproben automatisch sowohl die Ergebnisse des t-Tests bei Varianzhomogenität (Zeile „Varianzen sind gleich“) als auch bei Varianzheterogenität aus (Zeile „Varianzen sind nicht gleich“). Der Test, welcher bei Varianzheterogenität berichtet wird, wird auch als „Welch-Test“ bezeichnet, da es sich um einen t-Test mit „Welch-Korrektur“ handelt.
Da im Beispiel Varianzhomogenität vorliegt, wird die Zeile „Varianzen sind gleich“ betrachtet: Die Teststatistik beträgt t = -2.489 und der zugehörige Signifikanzwert p = .017. Damit ist der Unterschied signifikant: Die Mittelwerte der beiden Schulklassen unterscheiden sich (t(45) = -2.489, p = .017).
3.5. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel ist der Mittelwertsunterschied zwar signifikant, doch es stellt sich die Frage, ob der Unterschied gross genug ist, um ihn als bedeutend einzustufen.
Es gibt verschiedene Arten die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Der Korrelationskoeffizient eignet sich sehr gut, da die Effektstärke dabei immer zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Wenn sich jedoch die Gruppen hinsichtlich ihrer Grösse stark unterscheiden, wird empfohlen, d von Cohen zu wählen, da r durch die Grössenunterschiede verzerrt werden kann.
Zur Berechnung des Korrelationskoeffizienten r werden der t-Wert und die Freiheitsgrade (df) verwendet, die Abbildung 6 entnommen werden können:
Für das obige Beispiel ergibt das folgende Effektstärke:
Zur Beurteilung der Grösse des Effektes dient die Einteilung von Cohen (1992):
r = .10 entspricht einem schwachen Effekt
r = .30 entspricht einem mittleren Effekt
r = .50 entspricht einem starken Effekt
Damit entspricht eine Effektstärke von .35 einem mittleren Effekt.
3.6. Eine typische Aussage
Schulklasse B, die ein Training erhalten hat, schneidet im Gedächtnistest besser ab (M = 81.56, SD = 10.198, n = 25) als Schulklasse A (M = 74.32, SD = 9.668, n = 22), welche kein Training erhalten hat, t(45) = -2.489, p = .017. Die Effektstärke nach Cohen (1992) liegt bei r = .35 und entspricht damit einem mittleren Effekt.