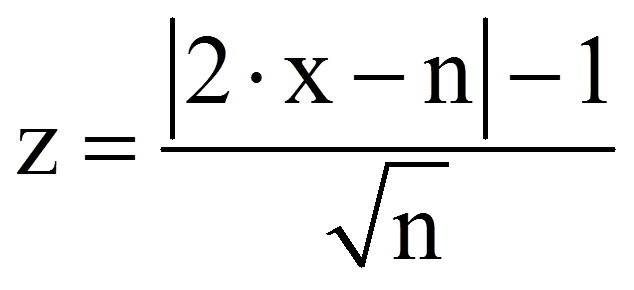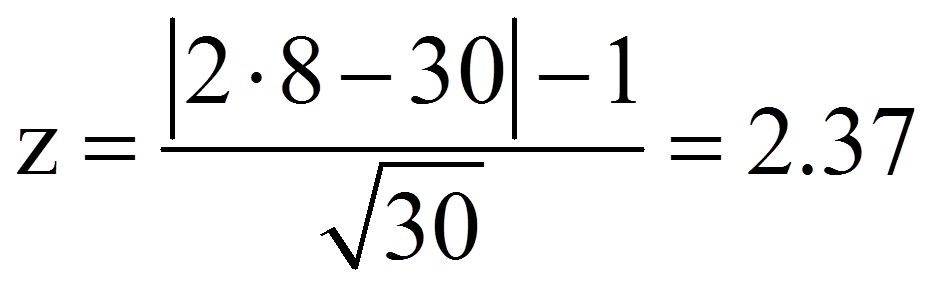 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen des Vorzeichentests
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Teststatistik
3. Der Vorzeichentest mit SPSS
3.1. SPSS-Befehle
3.2. Ergebnisse des Vorzeichentests
3.3. Eine typische Aussage
Quick Start
| Wozu wird der Vorzeichentest verwendet? Der Vorzeichentest für abhängige Stichproben testet, ob die zentralen Tendenzen zweier abhängiger Stichproben verschieden sind. Der Vorzeichentest wird verwendet, wenn die Voraussetzungen für einen t-Test für abhängige Stichproben nicht erfüllt sind. SPSS-Menü
Analysieren > Nichtparametrische Tests > Klassische Dialogfelder > Zwei verbundene Stichproben SPSS-Syntax
NPAR TESTS /SIGN = Variable1 WITH Variable2 (PAIRED) /STATISTICS = QUARTILES /MISSING = ANALYSIS. SPSS-Beispieldatensatz
Vorzeichentest |
1. Einführung
Der Vorzeichentest für abhängige Stichproben testet, ob die zentralen Tendenzen zweier abhängiger Stichproben verschieden sind. Der Vorzeichentest wird verwendet, wenn die Voraussetzungen für einen t-Test für abhängige Stichproben nicht erfüllt sind.
Von „abhängigen Stichproben“ wird gesprochen, wenn ein Messwert in einer Stichprobe und ein bestimmter Messwert in einer anderen Stichprobe sich gegenseitig beeinflussen. In drei Situationen ist dies der Fall:
- Messwiederholung: Die Messwerte stammen von der gleichen Person, zum Beispiel bei einer Messung vor und nach einem Treatment oder wenn verschiedene Treatments auf die gleiche Person angewandt werden und verglichen werden sollen.
- Natürliche Paare: Die Messwerte stammen von verschiedenen Personen, welche irgendwie zusammengehören (z.B.: Ehefrau – Ehemann, Psychologe – Patient, Anwalt – Klient, Eigentümer – Mieter oder Zwillinge).
- Matching: Die Messwerte stammen von verschiedenen Personen, die einander zugeordnet wurden, zum Beispiel aufgrund eines vergleichbaren Werts auf einer Drittvariablen (die nicht im Zentrum der Untersuchung steht).
Der Vorzeichentest ist das nichtparametrische Äquivalent des t-Tests für abhängige Stichproben und wird angewendet, wenn die Voraussetzungen für ein parametrisches Verfahren nicht erfüllt sind. Nicht-parametrische Verfahren sind auch bekannt als „voraussetzungsfreie Verfahren“, weil sie geringere Anforderungen an die Verteilung der Messwerte in der Grundgesamtheit stellen. So müssen die Daten nicht normalverteilt sein und die abhängige Variable muss lediglich ordinalskaliert sein. Auch bei kleinen Stichproben und Ausreissern kann ein Vorzeichentest berechnet werden.
Alternativ zum Vorzeichentest kann auch der Wilcoxon-Test ausgeführt werden. Der Vorzeichentest berechnet für alle Fälle die Differenzen zwischen den beiden Variablen und klassifiziert sie als positiv, negativ oder verbunden. Falls die beiden Variablen ähnlich verteilt sind, unterscheidet sich die Zahl der positiven und negativen Differenzen nicht signifikant. Der Wilcoxon-Test dagegen berücksichtigt sowohl Informationen über die Vorzeichen der Differenzen als auch die Grösse der Differenzen zwischen den Paaren. Da der Wilcoxon-Test mehr Informationen über die Daten aufnimmt, kann er mehr leisten als der Vorzeichentest.
Die Fragestellung des Vorzeichentests wird oft so verkürzt:
„Unterscheiden sich die zentralen Tendenzen zweier abhängiger Stichproben?“
1.1. Beispiele für mögliche Fragestellungen
- Verändert sich der Sauerstoffverbrauch nach einem Herz-Kreislauf-Training bei Kunstturnern?
- Verbessert sich die allgemeine Lebenszufriedenheit bei älteren Erwachsenen, nachdem sie ein Jahr im Turnverein tätig waren?
- Beurteilen Paare ihre Beziehungsqualität gleich?
1.2. Voraussetzungen des Vorzeichentests
| ✓ | Die abhängige Variable ist mindestens ordinalskaliert |
| ✓ | Es liegen zwei verbundene Stichproben oder Gruppen vor |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
Die Depressionswerte von 30 Patienten mit einer bipolaren Störung wurden vor Beginn einer medikamentösen Therapie und nach 6 Monate erhoben. Es soll ermittelt werden, ob sich nach einer 6-monatigen medikamentösen Behandlung bereits eine Besserung der Symptome zeigt.
Der zu analysierende Datensatz enthält neben einer Identifikationsnummer des Patienten (patient) die beiden Depressionswerte (vorher für die Erhebung vor der Behandlung, nachher für die Erhebung nach 6 Monaten).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
Berechnen der Teststatistik
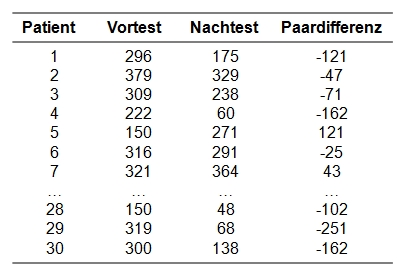
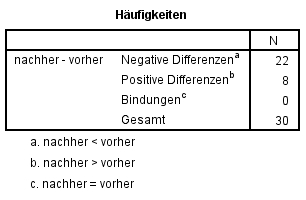
Die Berechnung der Teststatistik beruht auf den Vorzeichen der Paardifferenzen. Hierzu werden zunächst die Paardifferenzen berechnet. Im Beispiel wird vom Messwert nachher der Wert vorher subtrahiert (siehe Spalte „Paardifferenz“ in Abbildung 1). Anschliessend wird die Anzahl der positiven und der negativen Paardifferenzen gezählt. Im Beispiel sind dies 22 negative Differenzen und 8 positive Differenzen. Die Anzahl der positiven Differenzen wird als Teststatistik verwendet. Liegen „Bindungen“ vor – also Messwertpaare mit einer Differenz von 0 – so muss die Berechnung angepasst werden. Hierzu sei auf die Fachliteratur verwiesen.
Unterscheiden sich die zentralen Tendenzen nicht (Nullhypothese), so müsste die Anzahl der positiven und der negativen Paardifferenzen ungefähr gleich hoch sein. Unter Gültigkeit der Nullhypothese liegt die Wahrscheinlichkeit für eine positive Paardifferenz bei 50%. Damit liegt der Erwartungswert der Anzahl der positiven Paardifferenzen unter Gültigkeit der Nullhypothese bei n ∙ 0.5. Dies ist für das vorliegende Beispiel 30 ∙ 0.5 = 15.
Signifikanz der Teststatistik
Die Prüfung auf Signifikanz erfolgt anhand eines Binomialtests. Die Teststatistik – die berechnete Anzahl positiver Paardifferenzen – wird hierzu mit dem kritischen Wert der durch π = 0.5 charakterisierten Binomialverteilung verglichen. Ist die Stichprobe hinreichend gross, so kann gegen eine Normalverteilung getestet werden. Was „hinreichend gross“ bedeutet, wird unterschiedlich interpretiert; beispielsweise n ≥ 30 oder n ≥ 40 oder aber wenn der Erwartungswert der Anzahl der positiven Paardifferenzen ≥ 10 beträgt. SPSS prüft ab n = 26 gegen eine Normalverteilung. Dazu muss die Anzahl der positiven Differenzen z-standardisiert werden:
Dieser z-Wert kann nun auf Signifikanz geprüft werden, indem er mit dem kritischen Wert der Standardnormalverteilung (z-Verteilung) verglichen wird. Dieser kritische Wert kann Tabellen entnommen werden. Für das zweiseitige Signifikanzniveau .05 beträgt er ±1.96. Ist der Betrag der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel der Fall (2.27 > 1.96). Es kann also davon ausgegangen werden, dass sich die zentralen Tendenzen unterscheiden (Vorzeichentest: z = -2.37, p = .018, n = 30).
Ist die Stichprobe nicht hinreichend gross (n < 30), so muss der kritische Wert auf der Binomialverteilung bestimmt werden. Auf eine Darstellung der Berechnung wird an dieser Stelle verzichtet. Für weiterführende Informationen sei auf Statistiklehrbücher verwiesen. In SPSS wird zur Beurteilung bei n < 26 die exakte Signifikanz berichtet.
3. Der Vorzeichentest mit SPSS
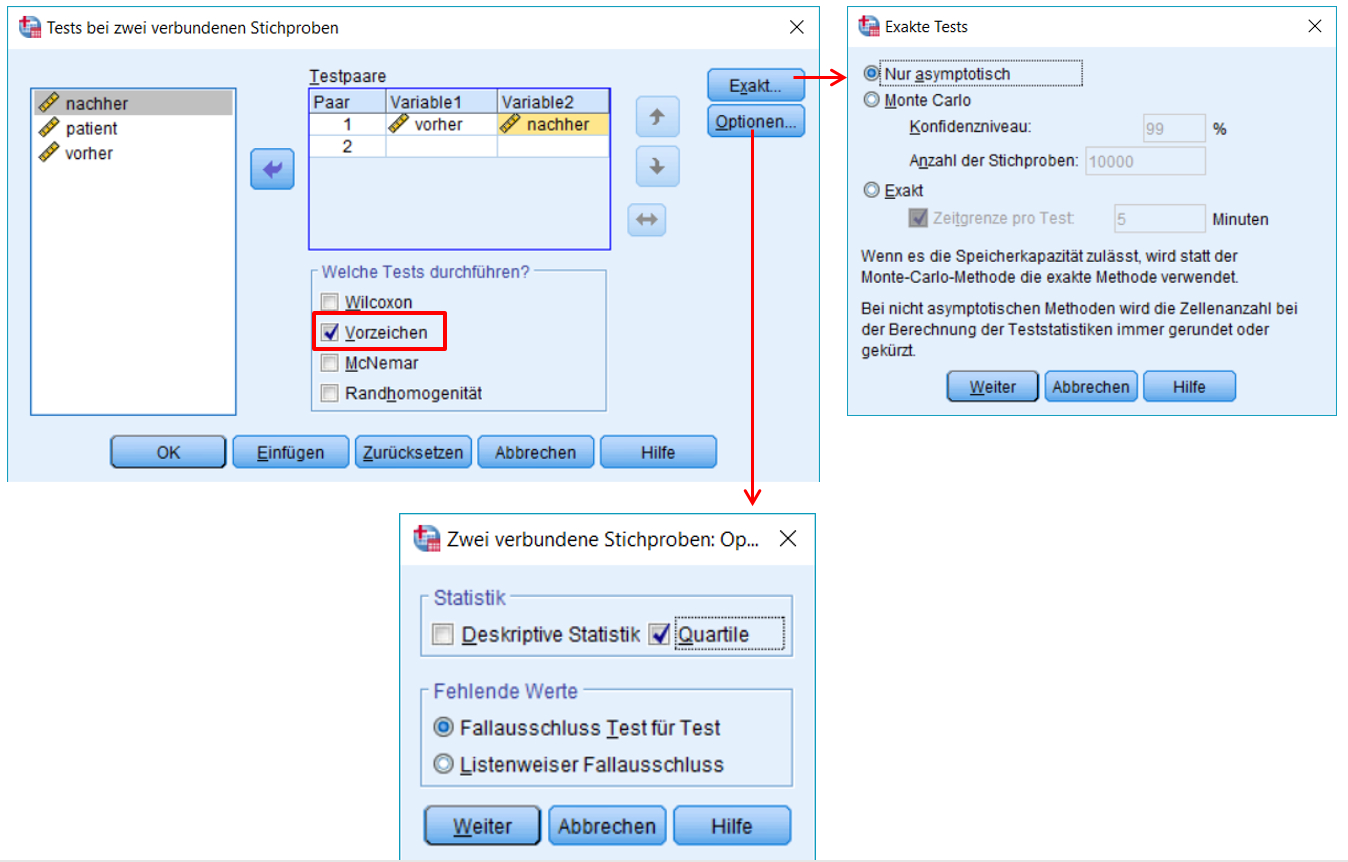
3.1. SPSS-Befehle
Hinweise
- Ab 26 Messwertpaaren berechnet SPSS die asymptotische Signifikanz. Bei n < 26 berichtet SPSS die exakte Signifikanz (ungeachtet der Wahl im Dialog).
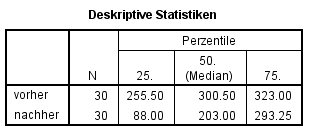
- Wird Quartile angewählt, so wird der Median für die beiden Messzeitpunkte / Treatments ausgegeben. Die ist für die Berichterstattung hilfreich.
SPSS-Syntax
NPAR TESTS
/SIGN = vorher WITH nachher (PAIRED)
/STATISTICS = QUARTILES
/MISSING = ANALYSIS.
Wie Abbildung 5 zeigt, unterscheiden sich die Depressionswerte vor und 6 Monate nach Beginn der medikamentösen Behandlung signifikant (z = -2.373, p = .018, n = 30).
3.3. Eine typische Aussage
Die Depressionswerte vor Beginn einer Behandlung (Mdn = 300.5) und 6 Monate später (Mdn = 203.0) unterscheiden sich signifikant (z = -2.373, p = .018, n = 30).