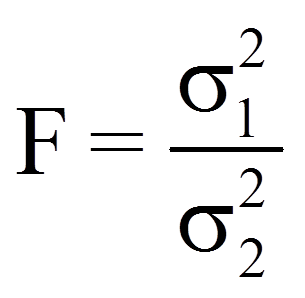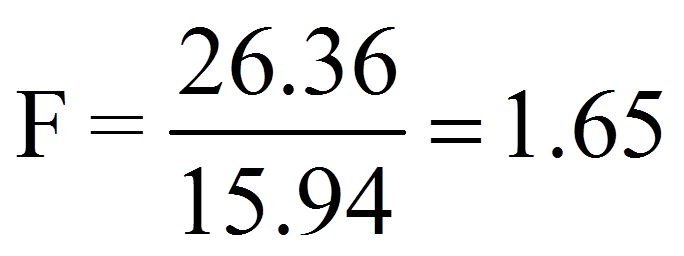 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen des F-Tests
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Teststatistik
3. Der F-Test mit SPSS
3.1. SPSS-Befehle
3.2. Ergebnisse via deskriptive Statistiken
3.3. Ergebnisse via t-Test für unabhängige Stichproben
3.4. Eine typische Aussage
Quick Start
| Wozu wird der F-Test verwendet? Der F-Test prüft, ob die Varianzen von zwei Stichproben homogen sind. SPSS-Menü
Analysieren > Deskriptive Statistiken > Häufigkeiten SPSS-Syntax
FREQUENCIES VARIABLES=Variable_Gruppe1 Variable_Gruppe2 /FORMAT=NOTABLE /STATISTICS=VARIANCE MEAN /ORDER=ANALYSIS. SPSS-Beispieldatensatz
F-Test |
1. Einführung
Der F-Test prüft, ob die Varianzen von zwei Stichproben im statistischen Sinne gleich sind, das heisst homogen, und folglich aus derselben Grundgesamtheit stammen. Der F-Test umfasst eine Gruppe statistischer Verfahren, bei denen die Teststatistik F-verteilt ist. Varianzhomogenität ist beispielsweise eine Voraussetzung des t-Tests für unabhängige Stichproben und bei Varianzanalysen (ANOVA). Der F-Test und Varianten davon, wie beispielsweise der Levene-Test, werden verwendet, um diese Voraussetzung zu prüfen.
Die Fragestellung des F-Tests wird oft so verkürzt:
„Unterscheiden sich die Varianzen eines interessierenden Merkmals in zwei unabhängigen Stichproben?“
1.1. Beispiele für mögliche Fragestellungen
- Unterscheiden sich Physik- und Psychologiestudierende hinsichtlich der Varianz ihres Intelligenzquotienten?
- Ist der Unterschied bezüglich der Varianz des Preises eines Produktes in zwei Detailhandelsgeschäften zufällig?
- Unterscheidet sich die Varianz der Dauer der täglichen Internetnutzung (in Stunden) bei jungen und älteren Erwachsenen?
1.2. Voraussetzungen des F-Tests
| ✓ | Die Variable ist intervallskaliert |
| ✓ | Die Variable weist in der Grundgesamtheit eine Normalverteilung auf |
| ✓ | Die zu vergleichenden Gruppen sind voneinander unabhängig |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
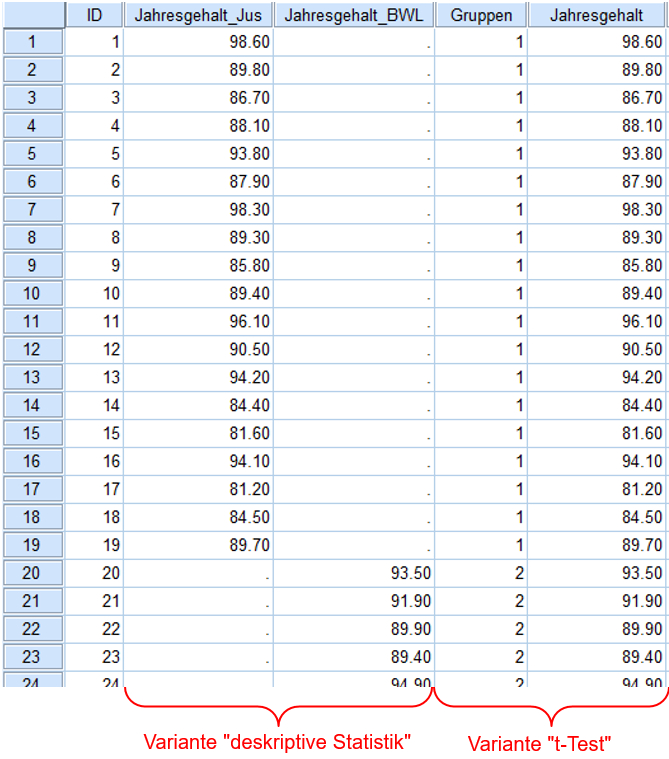
In einer Umfrage wurden je 19 Wirtschafts- und Juraabsolventen nach ihrem Einstiegsgehalt (Jahresgehalt in 1‘000 Franken) befragt. Es soll folgende Frage beantwortet werden: Unterscheiden sich die Varianzen des Einstiegsgehalts von Betriebswirtschafts- und Juraabsolventen?
Der zu analysierende Datensatz kann verschiedene Strukturen aufweisen:
Die erste Möglichkeit ist ein Datensatz – in Abbildung 1 als „Variante ‚deskriptive Statistik'“ bezeichnet –, der neben der Befragtennummer (ID) die Variablen Jahresgehalt_BWL sowie Jahresgehalt_Jus enthält, die für eine Person das Jahresgehalt enthalten oder einen fehlenden Wert, wenn die Person nicht zur entsprechenden Gruppe gehört. Diese Formatierung bietet sich an, wenn die Berechnung via deskriptive Statistiken erfolgen soll (siehe Kapitel 3.1).
Die zweite Möglichkeit ist ein Datensatz – in Abbildung 1 als „Variante ‚t-Test'“ bezeichnet – der neben der Befragtennummer (ID) eine Variable für die Gruppenzugehörigkeit (Gruppen) und eine für das Einstiegsgehalt (Jahresgehalt) enthält. Diese Formatierung bietet sich an, wenn die Berechnung via t-Test für unabhängige Stichproben erfolgen soll (siehe Kapitel 3.3).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
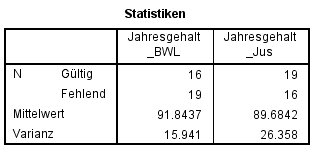
Abbildung 2 zeigt die Mittelwerte und Varianzen der abhängigen Variablen Jahresgehalt für die beiden Stichproben. Während die Mittelwerte sich nur geringfügig unterscheiden, ist die Differenz der Varianzen grösser. Bei Juraabsolventen zeigt sich eine geringere Streuung als bei Wirtschaftsabsolventen. Dieser Unterschied soll nun mittels F-Test auf Signifikanz geprüft werden.
Die Teststatistik des F-Tests wird folgendermassen berechnet:
Bei identischen Stichprobenvarianzen beträgt die F-Statistik den Wert 1. Bei F-Werten grösser oder kleiner als 1 unterscheiden sich die beiden Stichprobenvarianzen.
Signifikanz der Teststatistik
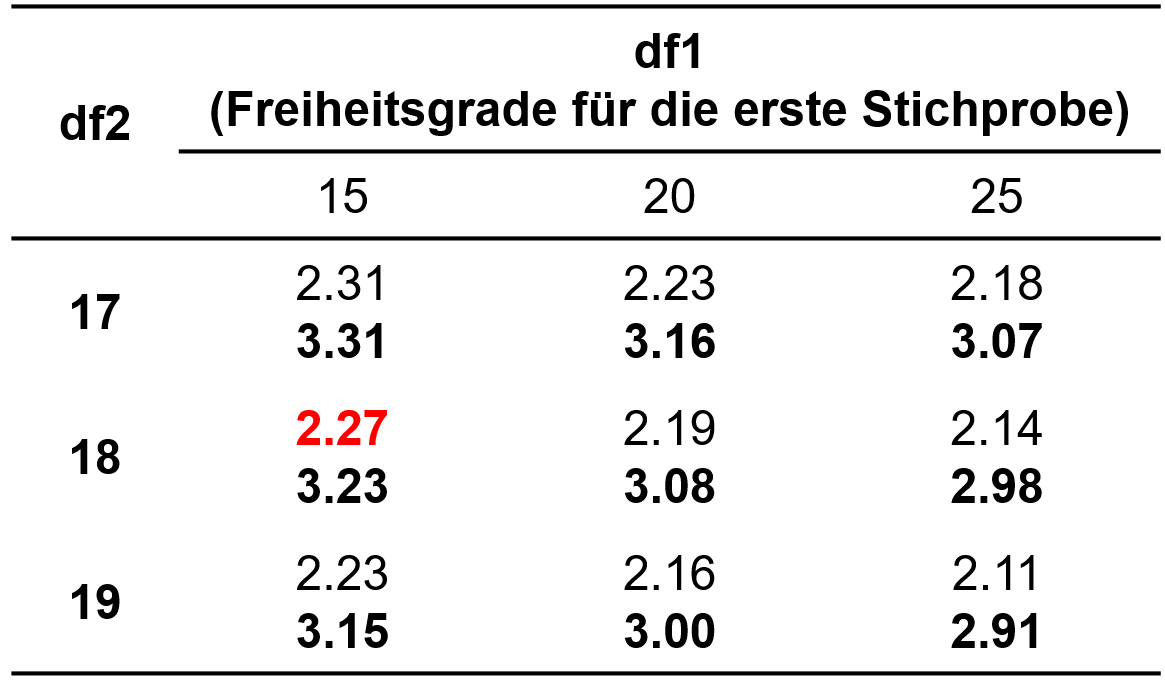
Der berechnete Wert muss nun auf Signifikanz geprüft werden. Dazu wird die Teststatistik mit dem kritischen Wert der durch die Freiheitsgrade bestimmten F-Verteilung verglichen. Dies sind im Falle der F-Verteilung zwei Freiheitsgrade: die Freiheitsgrade der Stichprobe mit der grösseren Varianz (auch Zählerfreiheitsgrade genannt, df1 ) und die Freiheitsgrade der Stichprobe mit der kleineren Varianz (auch Nennerfreiheitsgrade genannt, df2 ). Dieser kritische Wert kann Tabellen entnommen werden. Abbildung 3 zeigt einen Ausschnitt einer F-Tabelle, der die kritischen Werte der Signifikanzniveaus .05 und .01 zeigt.
Für das vorliegende Beispiel beträgt der kritische Wert 2.27 bei df1 = 15, df2 = 18 und α = .05 (siehe Abbildung 3). Ist der Wert der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel nicht der Fall (1.65 < 2.27). Es muss also davon ausgegangen werden, dass sich die Varianzen der Einstiegsgehälter der beiden Absolventengruppen nicht unterscheiden (F(15,18) = 1.65, p = .380, n = 35).
3. Der F-Test mit SPSS
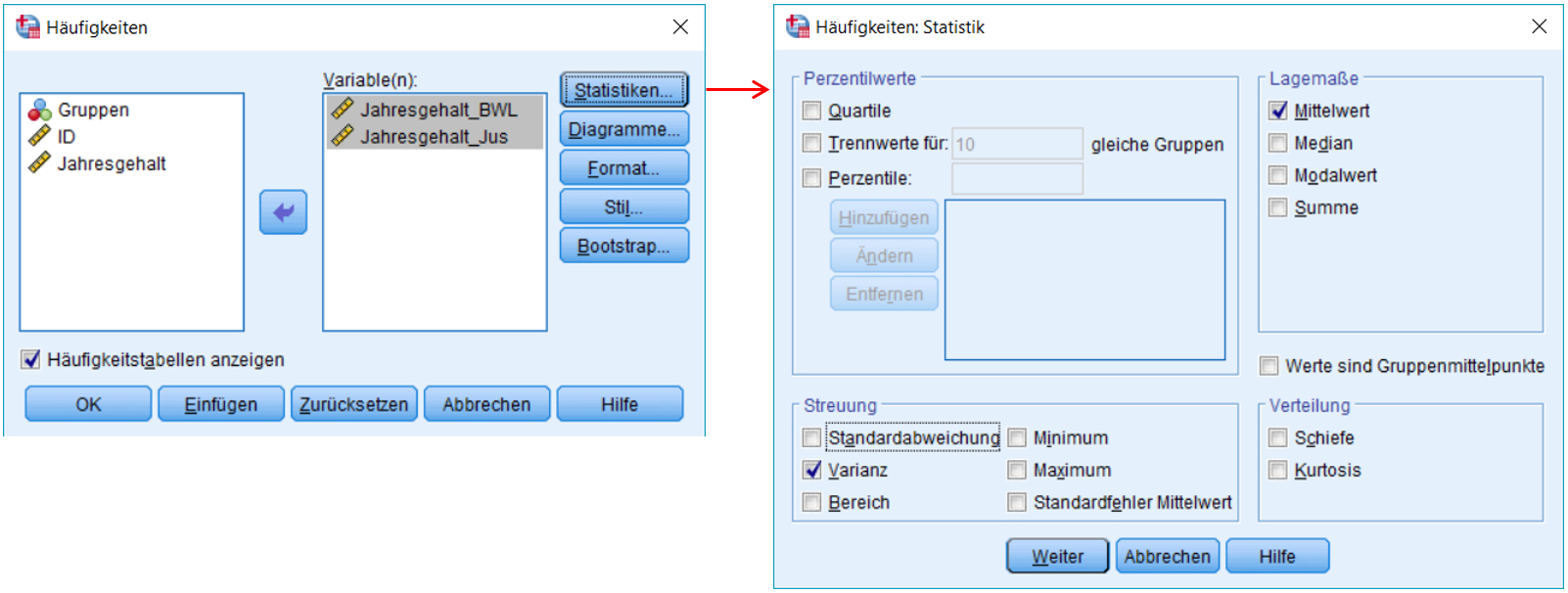
3.1. SPSS-Befehle
Es ist nicht möglich, den F-Test direkt mit SPSS durchzuführen. Entweder werden die Varianzen der beiden Stichproben mit Hilfe deskriptiver Statistiken ermittelt oder es wird ein Umweg über einen t-Test gegangen, wie weiter unten besprochen wird.
SPSS-Befehl via deskriptive Statistiken
SPSS-Menü: Analysieren > Deskriptive Statistiken > Häufigkeiten
Hinweis
- Unter Statistiken können die Kennwerte angegeben werden, die SPSS ausgeben soll. Zur manuellen Berechnung des F-Tests werden die Varianzen benötigt.
SPSS-Syntax
FREQUENCIES VARIABLES=Jahresgehalt_BWL Jahresgehalt_Jus
/FORMAT=NOTABLE
/STATISTICS=VARIANCE MEAN
/ORDER=ANALYSIS.
SPSS-Befehl via t-Test für unabhängige Stichproben
Wie der entsprechende SPSS-Befehl aufgebaut ist, lässt sich der Seite zum t-Test für unabhängige Stichproben entnehmen.
Unter Verwendung der Varianzen (Abbildung 5) lassen sich, wie im Unterkapitel Berechnung der Teststatistik beschrieben, der F–Wert und das zugehörige Signifikanzniveau bestimmen.
3.3. Ergebnisse via t-Test für unabhängige Stichproben
Wie Abbildung 6 zeigt, ist der Levene-Test nicht signifikant (p = .380). Dies bestätigt, dass sich die Varianzen der Einstiegsgehälter der beiden Absolventengruppen nicht unterscheiden (Levene-Test: F(1,33) = .792, p = .38, n = 35).
3.4. Eine typische Aussage
Die Varianzen des Einstiegsgehalts von Jura- und Wirtschaftsabsolventen unterscheiden sich nicht signifikant und es kann somit von homogenen Varianzen ausgegangen werden, wie ein Test unter Verwendung der deskriptiven Statistik zeigt (F(15,18) = 1.65,
p = .380, n = 35) respektive ein Levene-Test via t-Test zeigt (F(1,33) = .792, p = .380, n = 35).