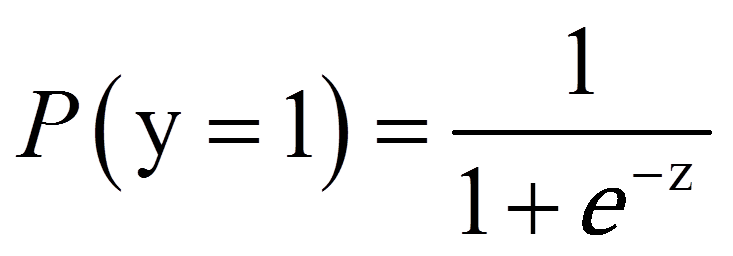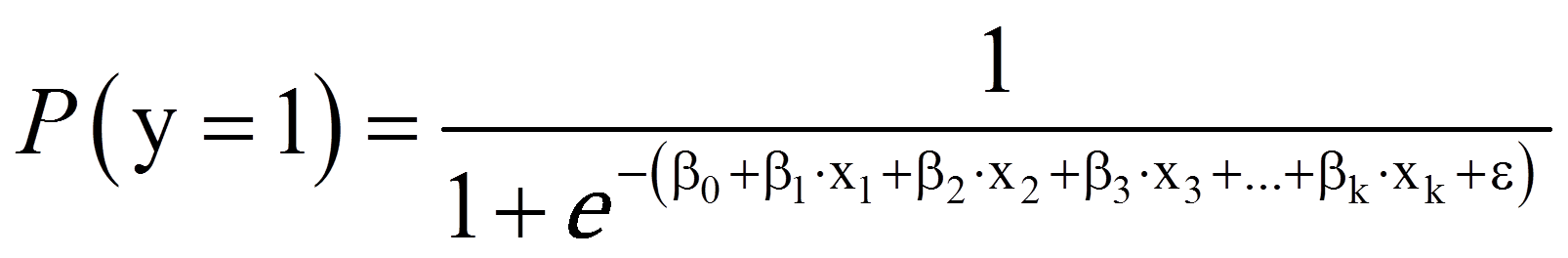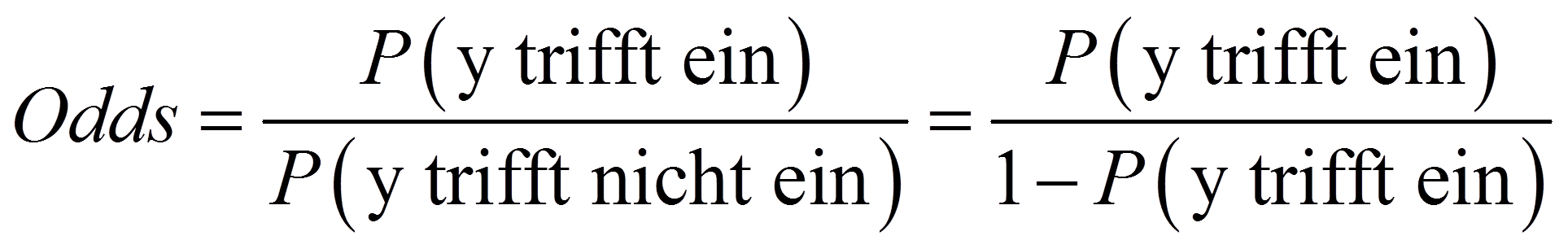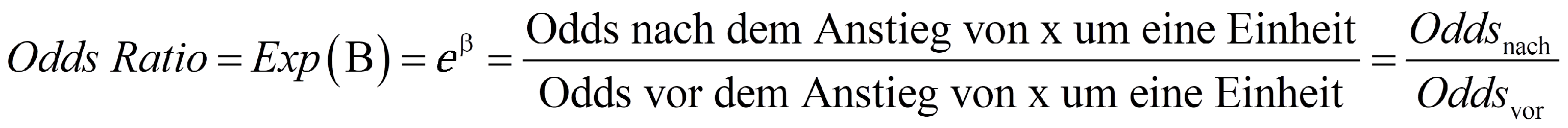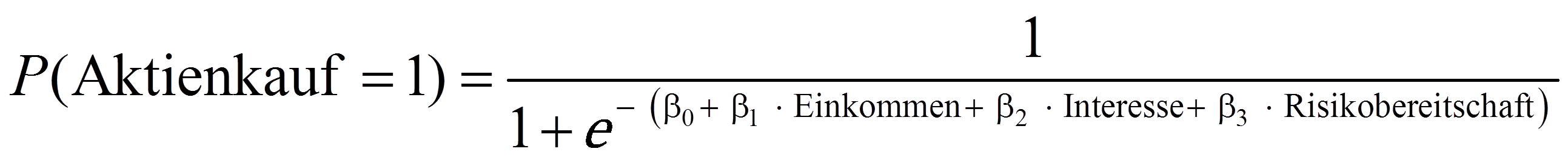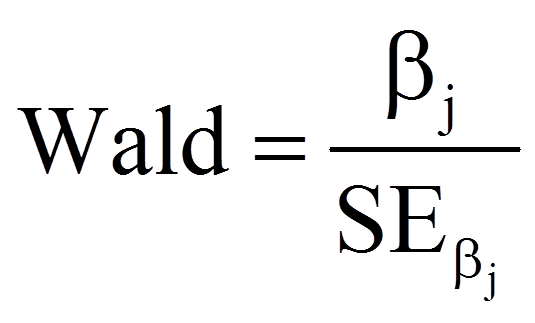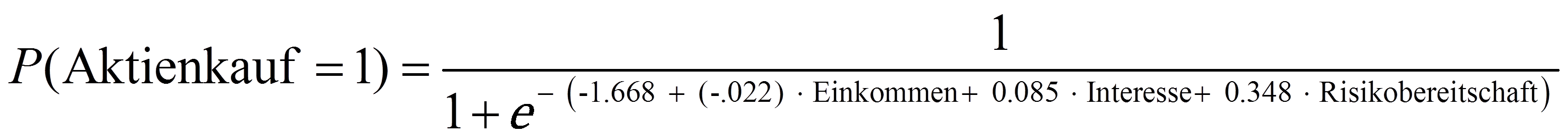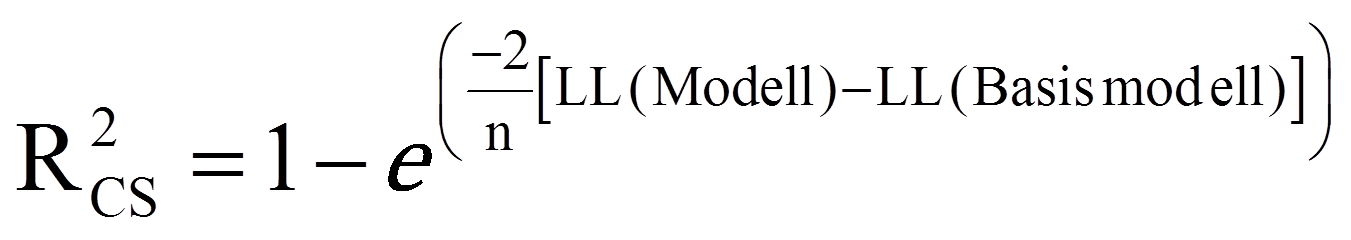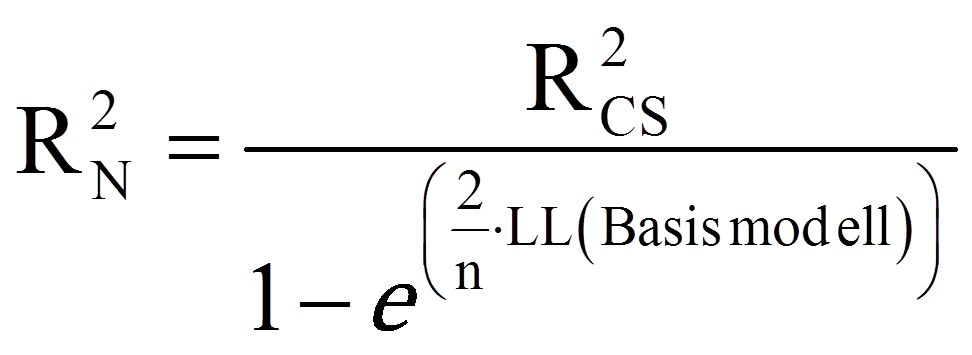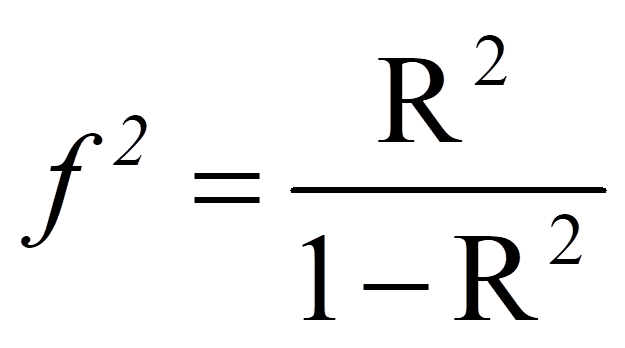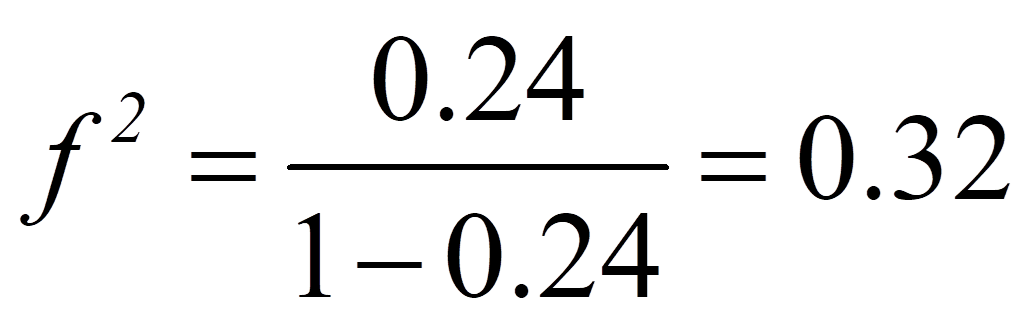 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Die Maximum-Likelihood-Schätzung
3. Logistische Regressionsanalyse mit SPSS
3.1. Formulierung des Regressionsmodells
3.2. Methoden des Variableneinschlusses
3.3. SPSS-Befehle
3.4. Signifikanz des Regressionsmodells
3.5. Signifikanz der Regressionskoeffizienten
3.6. Modellgüte
3.7. Berechnung der Effektstärke
3.8. Eine typische Aussage
Quick Start
| Wozu wird die logistische Regressionsanalyse verwendet? Die (binär) logistische Regressionsanalyse testet, ob ein Zusammenhang zwischen mehreren unabhängigen und einer binären abhängigen Variable besteht. SPSS-Menü
Analysieren > Regression > Binär logistisch SPSS-Syntax
LOGISTIC REGRESSION VARIABLES abhängige Variable /METHOD=ENTER unabhängige Variablen /CLASSPLOT /PRINT=ITER(1) CI(95) SPSS-Beispieldatensatz
Logistische Regression |
1. Einführung
Die (binär) logistische Regressionsanalyse wird angewandt, wenn geprüft werden soll, ob ein Zusammenhang zwischen einer abhängigen binären Variablen und einer oder mehreren unabhängigen Variablen besteht.
Im Unterschied zur einfachen Regressionsanalyse und multiplen Regressionsanalyse ist die abhängige Variable jedoch binär. Das heisst, sie hat nur zwei Ausprägungen; z.B. eine Variable Herzinfarkt, die die folgenden Ausprägungen annimmt: 1 für „ja, hat bereits einen Herzinfarkt gehabt“ und 0 für „nein, hat keinen Herzinfarkt gehabt“. Es wird dabei auch von „dichotomen“ Variablen gesprochen. Die unabhängigen Variablen hingegen sind intervallskaliert oder als Dummy-Variablen codiert.
Für ordinalskalierte abhängige Variablen und für nominale abhängige Variablen mit mehr als zwei Ausprägungen (z.B. die Variable Haarfarbe mit den Ausprägungen: braun, blond, schwarz oder rot) gibt es Erweiterungen der logistischen Regressionsanalyse: die ordinale logistische Regression und die multinominale logistische Regression. Auf diese wird jedoch nicht näher eingegangen.
Die binäre logistische Regressionsanalyse untersucht den Zusammenhang zwischen der Wahrscheinlichkeit, dass die abhängige Variable den Wert 1 annimmt und den unabhängigen Variablen. Das heisst, es wird nicht der Wert der abhängigen Variablen vorhergesagt, sondern die Wahrscheinlichkeit, dass die abhängige Variable den Wert 1 annimmt. Des Weiteren sind die Voraussetzungen weniger restriktiv als in der linearen Regressionsanalyse.
Es ist an dieser Stelle anzumerken, dass jeder postulierte Kausalzusammenhang theoretisch begründet sein muss.
Die Fragestellung der logistischen Regressionsanalyse wird oft so verkürzt:
„Haben die unabhängigen Variablen einen Einfluss auf die Wahrscheinlichkeit, dass die abhängige Variable den Wert 1 annimmt? Wie stark ist deren Einfluss?“
1.1. Beispiele für mögliche Fragestellungen
- Haben die Ernährung, die Sportlichkeit und das Stressempfinden einer Person einen Einfluss auf die Wahrscheinlichkeit eines Knochenmarkrückgangs (binäre Variable mit den Ausprägungen „Knochenmarkrückgang feststellbar“ und „kein Knochenmarkrückgang ersichtlich“)?
- Wie stark ist der Zusammenhang zwischen der Teilnahme an einer Weiterbildung und dem Selbstbewusstsein, der Führungsautorität des Arbeitgebers sowie dem Einkommen des potentiellen Teilnehmenden?
- Was beeinflusst die Wahrscheinlichkeit, dass Weihnachtsdekoration gekauft wird? Die Anzahl schneereicher Tage, die Aussentemperatur oder die Anzahl Tage bis zum 24. Dezember?
- Lässt sich die Wahrscheinlichkeit, dass eine bestimmte Fernsehsendung geschaut wird, durch das Geschlecht, das Alter, die Bildung und den Beruf vorhersagen?
1.2. Voraussetzungen
| ✓ | Die abhängige Variable ist binär (0-1-codiert) |
| ✓ | Die unabhängigen Variablen sind metrisch oder im Falle kategorialer Variablen als Dummy-Variablen codiert |
| ✓ | Für jede Gruppe, die durch kategoriale Prädiktoren gebildet wird, ist n ≥ 25 |
| ✓ | Die unabhängigen Variablen sind untereinander nicht hoch korreliert |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
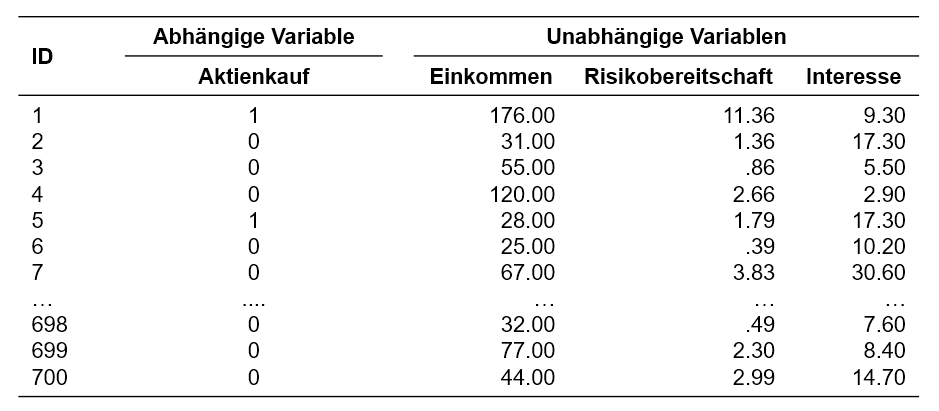
Eine Bank interessiert sich für Fakten, die mit der Wahrscheinlichkeit, dass jemand Aktien erwirbt, zusammenhängen. Sie beauftragt daher ein Marktforschungsinstitut, 700 Personen zu befragen. Es wird angenommen, dass der Entscheid für einen Aktienkauf vom Jahreseinkommen (in Tausend CHF), der Risikobereitschaft (Skala von 0 bis 25) sowie vom Interesse an der aktuellen Marktlage (Skala von 0 bis 45) beeinflusst wird.
Der zu analysierende Datensatz enthält daher neben einer Befragtennummer (ID) eine Variable zum Aktienkauf (Aktienkauf: 0 nein, 1 ja), das Jahreseinkommen (Einkommen), die Risikobereitschaft (Risikobereitschaft) und das Interesse an der aktuellen Marktlage (Interesse).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Die Maximum-Likelihood-Schätzung
Das logistische Regressionsmodell
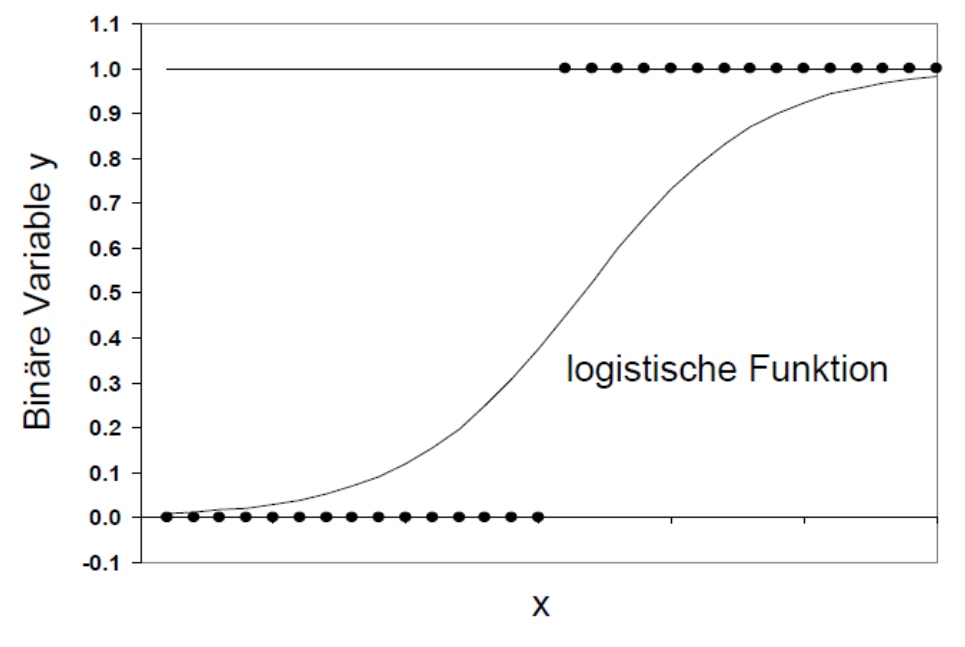
Die logistische Regressionsanalyse basiert auf der Maximum-Likelihood-Schätzung (auch MLE genannt, denn engl. „Maximum-likelihood estimation“) und unterscheidet sich von der Methode der kleinsten Quadrate, die bei linearen Regressionsanalysen angewendet wird. Ähnlich wie bei einer linearen Regressionsanalyse wird versucht, eine Funktionskurve zu finden, die möglichst gut zu den Daten passt. Diese Funktion ist jedoch im Gegensatz zur linearen Regressionsanalyse keine Gerade, sondern eine logistische Funktion (siehe Abbildung 2). Sie ist „s-förmig“, symmetrisch und verläuft asymptotisch gegen y = 0 und y = 1. Das heisst, die logistische Funktion nimmt nur Werte zwischen 0 und 1 an.
Die Werte der logistischen Funktion werden als Wahrscheinlichkeit interpretiert, dass die abhängige Variable y den Wert 1 annimmt (gegeben die unabhängigen Variablen xk), denn mittels eines logistischen Regressionsmodells werden nicht die Werte der abhängigen Variablen y vorhergesagt werden, sondern die Eintrittswahrscheinlichkeit von y. Ein Wert nahe bei 0 bedeutet, dass das Eintreten von y (y = 1) sehr unwahrscheinlich ist, während ein Wert nahe bei 1 bedeutet, dass das Eintreten von y sehr wahrscheinlich ist.
Die logistische Regressionsfunktion ist wie folgt:
Maximum-Likelihood-Schätzung
Die Regressionskoeffizienten werden durch den Algorithmus der Maximum-Likelihood-Schätzung (MLE) geschätzt. MLE bestimmt die Regressionsparameter so, dass sie für die beobachteten y-Werte möglichst hohe Wahrscheinlichkeiten voraussagt, wenn y = 1 und möglichst tiefe Wahrscheinlichkeiten, wenn y = 0 ist. MLE maximiert dabei eine „Likelihood-Funktion“, die aussagt, wie wahrscheinlich es ist, dass der Wert einer abhängigen Variablen durch die unabhängigen Variablen vorausgesagt werden kann. Der Wert der Likelihood-Funktion kann zur Einschätzung der Modellgüte und Modellsignifikanz verwendet werden, wie weiter unten ersichtlich werden wird.
Interpretation der Regressionskoeffizienten
Die Regressionskoeffizienten werden im Rahmen der logistischen Regression nicht mehr gleich interpretiert, wie dies in der linearen Regression der Fall war. Ein Blick auf die logistische Regressionsfunktion zeigt, dass der Zusammenhang nicht linear ist, sondern komplexer. Was nach wie vor gilt, ist die „Vorzeicheninterpretation“: Ist das Vorzeichen eines Regressionskoeffizienten positiv, so bewirkt ein Anstieg der betreffenden unabhängigen Variablen einen Anstieg der Wahrscheinlichkeit, dass y = 1. Ist das Vorzeichen negativ, so bedeutet dies eine Abnahme der Wahrscheinlichkeit.
Genauer kann der Zusammenhang zwischen einer unabhängigen Variablen und der abhängigen Variablen mittels sogenannter „Odds“ (oder: Wettquoten) interpretiert werden. Zur Berechnung der Odds wird die Wahrscheinlichkeit, dass das Ereignis eintrifft, in Relation zum Nichteintreffen des Ereignisses gestellt. Odds werden folgendermassen berechnet:
Zur Interpretation eines Regressionskoeffizienten werden sogenannte „Odds Ratios“ beigezogen. Diese sind das Verhältnis zweier Odds. SPSS bezeichnet die Odds Ratio einer Variablen als „Exp(B)“, da sie auch als eβ berechnet werden können (β steht für den Regressionskoeffizienten, e für die Eulersche Zahl). SPSS gibt Odds Ratios des folgenden Typs aus:
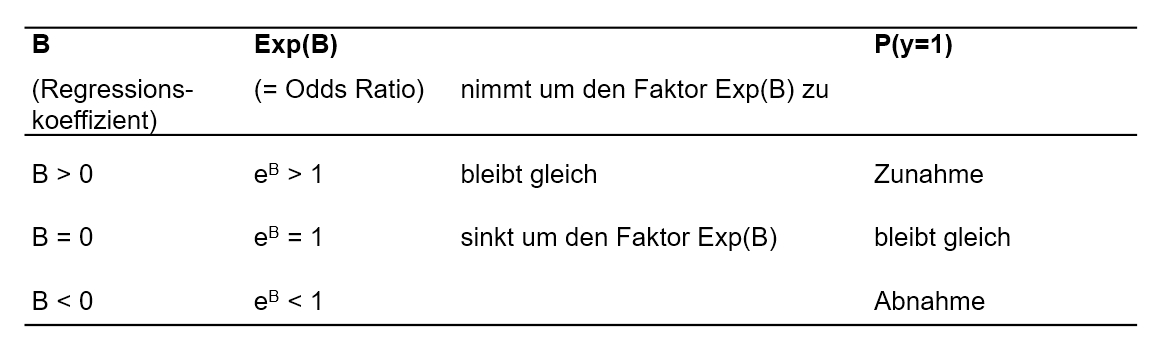
Die Odds Ratio einer unabhängigen Variablen geben die Veränderung der relativen Wahrscheinlichkeit von y = 1 an, wenn diese unabhängige Variable um eine Einheit steigt, gegeben alle anderen Variablen im Modell werden konstant gehalten. Das heisst, die Odds Ratio einer unabhängigen Variablen ist der Faktor, um den sich die Odds verändern, wenn diese Variable um eine Einheit ansteigt. Beträgt also eine Odds Ratio (Exp(B)) eins, so ergibt das eine Multiplikation der relativen Wahrscheinlichkeit mit 1 und damit keine Veränderung (Oddsnach = Oddsvor). Ist die Odds Ratio > 1, so bedeutet dies eine Zunahme der Odds (Oddsnach > Oddsvor), während eine Odds Ratio < 1 eine Abnahme der Odds bedeutet (Oddsnach < Oddsvor).
Über die Beziehung Odds Ratio = Exp(B) = eβ zeigt sich, wie Odds Ratios und Regressionskoeffizienten zusammenhängen: Eine Odds Ratio ist 1, wenn der Regressionskoeffizient 0 beträgt (B = 0), > 1, wenn der Regressionskoeffizient positiv ist (B > 0), und < 1, wenn der Regressionskoeffizient negativ ist (B < 0). Abbildung 3 gibt einen Überblick:
3. Logistische Regressionsanalyse mit SPSS
3.1. Formulierung des Regressionsmodells
Bei der Formulierung des Regressionsmodells muss entschieden werden, welche Variablen als abhängige und als unabhängige Variablen ins Modell einfliessen. Dabei spielen theoretische Überlegungen eine zentrale Rolle. Das Modell sollte möglichst einfach gehalten werden. Daher empfiehlt es sich, nicht zu viele unabhängige Variablen aufzunehmen. Im Falle des vorliegenden Beispiels ist Aktienkauf die abhängige Variable, deren Eintrittswahrscheinlichkeit durch Einkommen, Interesse und Risikobereitschaft vorhergesagt wird:
3.2. Methoden des Variableneinschlusses
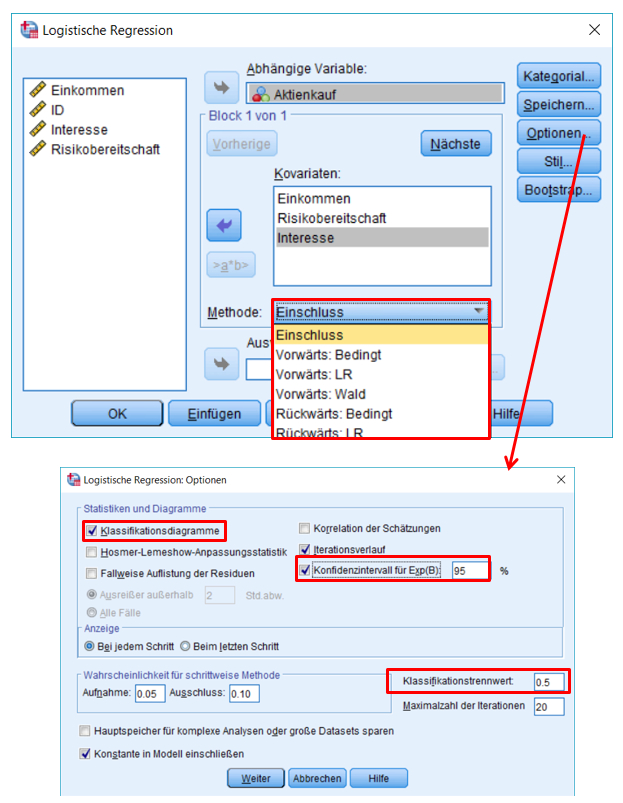
Vor der Durchführung der Analyse muss entschieden werden, in welcher Reihenfolge die unabhängigen Variablen in das Modell aufgenommen werden sollen. Dies kann einen Einfluss auf das Modell haben, das am Ende der Analyse berichtet wird. Sind alle unabhängigen Variablen vollständig unkorreliert, so spielt die Reihenfolge, in der sie in das Modell eingeführt werden, keine Rolle. In den Sozialwissenschaften sowie in der Marktforschung sind die Variablen jedoch selten vollständig unkorreliert. Somit ist die Methode des Variableneinschlusses relevant.
Methoden des Variableneinschlusses in SPSS
SPSS bietet verschiedene Vorgehensweisen an, um die unabhängigen Variablen in das Modell aufzunehmen (vgl. Klicksequenz in Abbildung 4).
- Einschluss (ENTER): Eine Prozedur für die Variablenauswahl, bei der alle Variablen eines Blocks in einem einzigen Schritt aufgenommen werden.
- Vorwärtsauswahl (Bedingt): Eine Methode der schrittweisen Variablenauswahl mit einem Test auf Aufnahme, der auf der Signifikanz der Scorestatistik beruht, und einem Test auf Ausschluss, der auf der Wahrscheinlichkeit einer Likelihood-Quotienten-Statistik beruht, die mit bedingten Parameterschätzungen berechnet wird.
- Vorwärtsauswahl (Likelihood-Quotient): Eine Methode der schrittweisen Variablenauswahl mit einem Test auf Aufnahme, der auf der Signifikanz der Scorestatistik beruht, und einem Test auf Ausschluss, der auf der Wahrscheinlichkeit einer Likelihood-Quotienten-Statistik beruht. Diese basiert hier auf Schätzwerten, die aus dem Maximum einer partiellen Likelihood-Funktion ermittelt werden.
- Vorwärtsauswahl (Wald): Eine Methode der schrittweisen Variablenauswahl mit einem Test auf Aufnahme, der auf der Signifikanz der Scorestatistik beruht, und einem Test auf Ausschluss, der auf der Wahrscheinlichkeit der Wald-Statistik beruht.
- Rückwärts LR: Die Rückwärts-Selektion stellt die Umkehrung der Vorwärts-Selektion dar. Schritt für Schritt werden unabhängige Variablen aus dem Modell entfernt, wobei mit derjenigen gestartet wird, welche den geringsten Zusammenhang zur abhängigen Variable aufweist. Gleichzeitig wird mittels der Likelihood-Ratio-Statistik geprüft, ob sich das Modell durch erneutes Hinzufügen einer Variablen verbessern würde. (Die Methoden „Rückwärts Wald“ und „Rückwärts bedingt“ werden nicht empfohlen.)
- Rückwärtselimination (Bedingt). Rückwärtsgerichtete schrittweise Auswahl. Der Aus-schlusstest basiert auf der Wahrscheinlichkeit der Likelihood-Quotienten-Statistik auf der Grundlage bedingter Parameterschätzungen.
- Rückwärtselimination (Likelihood-Quotient). Rückwärtsgerichtete schrittweise Auswahl. Der Ausschlusstest basiert auf der Wahrscheinlichkeit der Likelihood-Quotienten-Statistik auf der Grundlage maximaler, partieller Likelihood-Schätzungen.
- Rückwärtselimination (Wald). Rückwärtsgerichtete schrittweise Auswahl. Der Ausschluss-test basiert auf der Wahrscheinlichkeit der Wald-Statistik.
Im vorliegenden Beispiel beruht das Regressionsmodell auf fundierten theoretischen Überlegungen, weswegen die „Einschluss“-Methode gewählt wird.
Hierarchische Regressionsanalyse
Zusätzlich können Variablen auch in Blöcken eingeführt werden (daher engl. auch „blockwise regression“). Dies ist den bisher beschriebenen Vorgehensweisen übergeordnet und kann beliebig mit diesen kombiniert werden. Dabei werden mehrere Variablengruppen (Blöcke) vorgegeben, die SPSS nacheinander in das Modell aufnimmt. Innerhalb von jedem Block wird die bereits gewählte Methode angewendet (z.B. „Einschluss“ oder „Vorwärts LR“). In einer Studie zum Einfluss des Umweltbewusstseins auf das Verhalten könnte beispielsweise mit dem ersten Block ein Modell gebildet werden, das soziodemographische Variablen beinhaltet. Im zweiten Block wird dann das Umweltbewusstsein eingeführt. In SPSS werden dabei nicht alle Variablen gleichzeitig in die Box „Kovariaten“ eingetragen, sondern lediglich jene des ersten Blocks. Dann wird „Weiter“ gewählt und die Variablen des zweiten Blocks werden eingefügt, etc.
Dieses Vorgehen hat zwei Vorteile: Erstens kann auf diese Weise die Reihenfolge des Variableneinschlusses genau vorgegeben werden. Zweitens gibt SPSS für jeden Schritt, also nach jedem Block, ein Regressionsmodell aus. Dadurch kann die Veränderung von Regressionskoeffizienten durch die Aufnahme einer bestimmten weiteren Variablen beobachtet werden und es können Tests durchgeführt werden, ob sich das Modell durch das Hinzufügen des weiteren Blocks verbessert.
Im Rahmen des vorliegenden Beispiels werden alle Variablen im ersten Block eingefügt, um das Beispiel möglichst einfach zu halten.
3.3. SPSS-Befehle
SPSS-Menü: Analysieren > Regression > Binär logistisch
Hinweise
- Bei Methode wird entschieden, wie die unabhängigen Variablen in das Modell aufgenommen werden.
- Unter Optionen finden sich die Klassifikationsdiagramme und Konfidenzintervalle für Exp(B).
- Die Standardeinstellung des Klassifikationsschwellenwerts liegt bei 0.5.
SPSS-Syntax
LOGISTIC REGRESSION VARIABLES Aktienkauf
/METHOD=ENTER Einkommen Interesse Risikobereitschaft
/CLASSPLOT
/PRINT=ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).
3.4. Signifikanz des Regressionsmodells
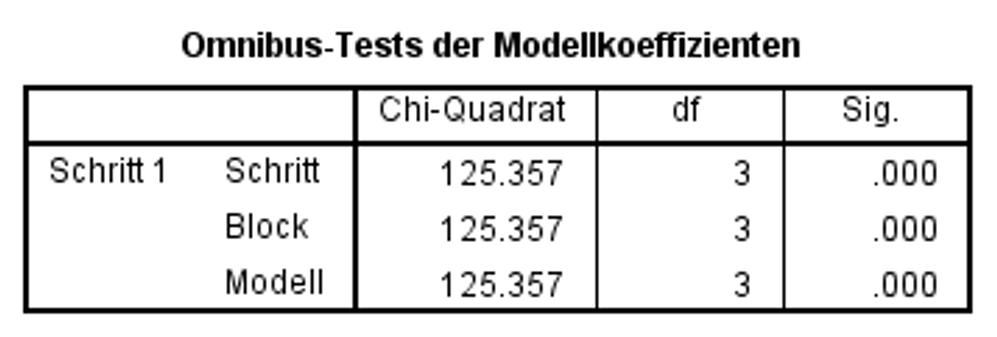
Zur Überprüfung, ob das Regressionsmodell insgesamt signifikant ist, wird ein Chi-Quadrat-Test durchgeführt (in SPSS als „Omnibus-Test der Modellkoeffizienten“ bezeichnet). Dieser prüft, ob das Modell insgesamt einen Erklärungsbeitrag leistet gegenüber der modalen Vorhersage (für alle Personen wird der modale Wert von y vorhergesagt). Dazu verwendet dieser Test den Logarithmus des Werts der Likelihood-Funktion, welche im Zuge der Modellschätzung maximiert wurde (siehe Die Maximum-Likelihood-Schätzung). Dieser logarithmierte Wert wird als „Log-Likelihood“ oder kurz „LL“ bezeichnet. Für die Schätzung der Modellgüte wird dieser Wert mit -2 multipliziert (-2LL). Der Wert -2LL beschreibt einen Fehlerterm. Im Rahmen des Signifikanztests werden die -2LL-Werte zweier Modelle verglichen: jener des aufgestellten Regressionsmodells und jener des sogenannten „Basismodells“. Das Basismodell ist ein Modell, welches nur die Konstante berücksichtigt. SPSS gibt den Wert -2LL des postulierten Modells in der Tabelle „Modellzusammenfassung“ aus (siehe Abbildung 7), während der Wert -2LL des Basismodells ausgegeben wird, wenn unter „Optionen“ das „Iterationsprotokoll“ angefordert wird. Die auf diesem Vergleich basierende Testgrösse folgt einer Chi-Quadrat-Verteilung:
mit
Das heisst, die Signifikanz der Teststatistik Chi-Quadrat kann geprüft werden, indem die Teststatistik mit dem kritischen Wert auf einer durch die entsprechende Anzahl Freiheitsgrade definierten Chi-Quadrat-Verteilung verglichen wird.
In der Zeile „Modell“ in Abbildung 5 ist zu erkennen, dass das Modell als Ganzes signifikant ist (Chi-Quadrat(3) = 125.36, p < .001). Aus diesem Grund kann die Analyse fortgesetzt werden. Wäre das Modell als Ganzes nicht signifikant, so würde die Analyse nicht fortgesetzt.
Diese Tabelle (Abbildung 5) beinhaltet neben der Zeile „Modell“ weitere Zeilen. Diese sind nur bedeutsam, wenn unter „Methode“ nicht „Einschluss“ verwendet wird oder wenn eine hierarchische Regressionsanalyse durchgeführt wird.
3.5. Signifikanz der Regressionskoeffizienten
Nun wird geprüft, ob die Regressionskoeffizienten (Betas) ebenfalls signifikant sind. Dabei wird für jeden der Regressionskoeffizienten ein Wald-Test durchgeführt. Die Teststatistik des Wald-Tests wird folgendermassen berechnet:
mit
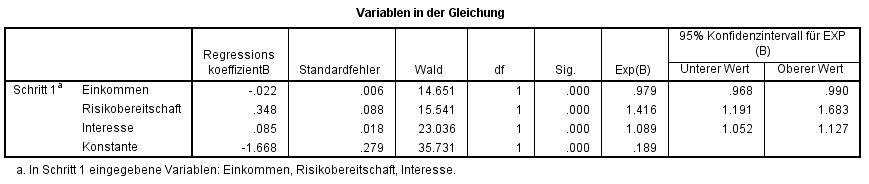
| = | Regressionskoeffizient der Variable xj (siehe Spalte „RegressionskoeffizientB“ in Abbildung 6) | |
| = | Standardfehler von β (siehe Spalte „Standardfehler“ in Abbildung 6) |
Die Ergebnisse der Wald-Tests können den Spalten „Wald“ und „Sig.“ in Abbildung 6 entnommen werden. SPSS berichtet in der Spalte „Wald“ das Quadrat der Wald-Teststatistik.
Abbildung 6 zeigt, dass die z-Tests für den Regressionskoeffizienten von Einkommen (Wald(1) = 14.651, p < .001), von Interesse (Wald(1) = 23.036, p < .001), von Risikobereitschaft (Wald(1) = 15.541, p < .001) und die Konstante β (Wald(1) = 35.731, p < .001) signifikant ausfallen. Die signifikanten Koeffizienten der unabhängigen Variablen bedeuten, dass deren Regressionskoeffizienten nicht 0 sind und diese Variablen somit einen signifikanten Einfluss auf Aktienkauf aufweisen.
Da der Einfluss der Variablen über die Odds Ratios (Exp(B)) interpretiert wird, wird ihre Signifikanz ebenfalls geprüft: Schliesst das Konfidenzintervall von Exp(B) den Wert 1 nicht ein, so wird von einem signifikanten Einfluss ausgegangen. Dies trifft bei allen untersuchten unabhängigen Variablen zu (siehe Abbildung 6, Spalten „95% Konfidenzintervall für EXP(B)“).
Somit ergibt sich folgende Regressionsfunktion:
Bei Risikobereitschaft und Interesse ist der Wert von Exp(B) > 1 (und das Vorzeichen von B entsprechend positiv). Deshalb gilt: Steigt die Risikobereitschaft um eine Einheit an, so steigt die relative Wahrscheinlichkeit, dass eine Person bereits einmal Aktien gekauft hat, um 41.6% (1.416 – 1 = .416). Steigt das Interesse um eine Einheit, so nimmt die relative Wahrscheinlichkeit, dass eine Person bereits einmal Aktien erworben hat, um 8.9% zu (1.089 – 1 = .089). Für Einkommen ist Exp(B) < 1 (und das Vorzeichen von B entsprechend negativ). Das bedeutet: Steigt das Einkommen um eine Einheit (1’000 Schweizer Franken), so sinkt die relative Wahrscheinlichkeit, dass eine Person bereits einmal Aktienkäufe getätigt hat, um 2.1% (.979 – 1 = -.021).
3.6. Modellgüte
Zur Beurteilung der Modellgüte werden im Rahmen der logistischen Regression Analogien zum R2 der linearen Regression verwendet. Es gibt eine grosse Anzahl verschiedener solcher Pseudo-R2 – zwei davon sind in SPSS implementiert: das Cox und Snell R2 und das Nagelkerke R2. Das Cox und Snell R2 berechnet sich wie folgt:
Das Nagelkerke R2 für das vorliegende Beispiel liegt, wie Abbildung 7 abgelesen werden kann, bei .24.
Vorhergesagte Wahrscheinlichkeiten und beobachtete Werte
Die logistische Regressionsfunktion berechnet Wahrscheinlichkeiten, dass die abhängige Variable den Wert 1 annimmt. Diese Wahrscheinlichkeiten variieren zwischen 0 und 1. Diese Informationen können verwendet werden, um das Ergebnis genauer zu betrachten, wenn unter „Optionen“ die „Klassifikationsdiagramme“ angewählt wurden (oder alternativ – hier nicht näher erläutert – wenn die vorhergesagten Wahrscheinlichkeiten als Variablen gespeichert wurden und anschliessend separat analysiert werden).
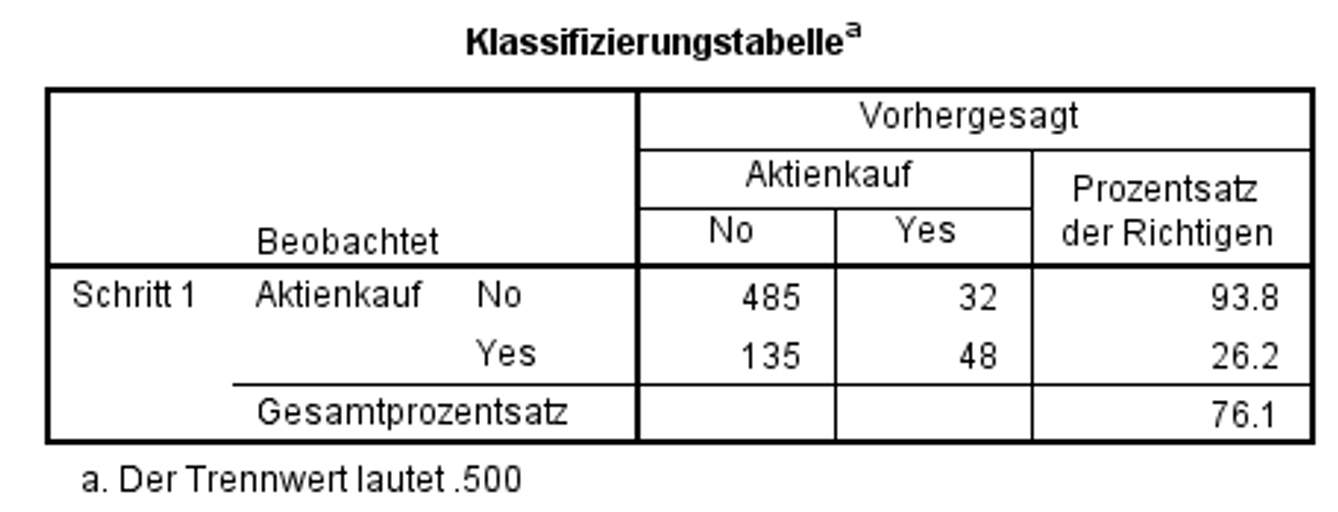
SPSS nutzt die Wahrscheinlichkeit von 50.0% (0.500, siehe Fussnote in Abbildung 8) als Trennwert, um festzulegen, ob y = 0 oder y = 1 vorausgesagt wird. Ab einer vorhergesagten Wahrscheinlichkeit von 0.500 wird also vorhergesagt, dass Aktienkauf = 1 ist. Bei einer geringeren Wahrscheinlichkeit wird Aktienkauf = 0 prognostiziert. Sind die Anteile für y = 0 oder y = 1 gleich gross, kann ein Trennwert von 0.500 gewählt werden, andernfalls entspricht er dem Anteil der Fälle y = 1 und kann aus der Klassifizierungstabelle des Anfangsblocks herausgelesen werden. Der Trennwert kann in SPSS unter „Optionen“ bei „Klassifizierungsschwellenwert“ festgelegt werden. Das Ergebnis mit der Standardeinstellung 0.500 kann Abbildung 8 entnommen werden:
Insgesamt wurden 76.1% der Personen durch das Modell entsprechend ihrer tatsächlichen Antwort klassifiziert. Von denjenigen Personen, die noch nie Aktien gekauft haben, wurden 485 von insgesamt 517 (485 + 32) richtig vorhergesagt. Dies entspricht 93.8% korrekten Prognosen. Von denjenigen Personen, die Aktien erworben haben, wurden nur 48 von insgesamt 183 (135 + 48) Aktienkäufen korrekt vorhergesagt. Dies entspricht 26.2% korrekten Prognosen.
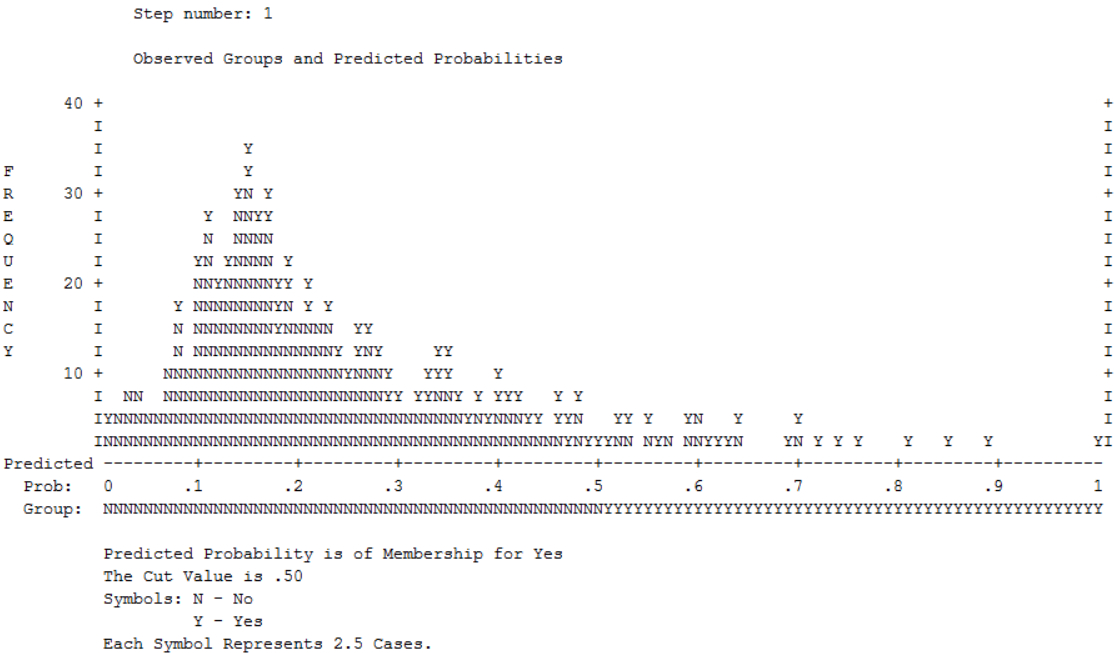
Das „Diagramm der beobachteten Gruppen und vorhergesagten Wahrscheinlichkeiten“ stellt eine Art Histogramm dar und illustriert ebenfalls den Zusammenhang zwischen vorhergesagten Wahrscheinlichkeiten, entsprechend klassifizierten Vorhersagen für y und den beobachteten Werten (Abbildung 9).
Die Buchstaben im Diagramm repräsentieren Beobachtungen (ob jeder Buchstabe für eine oder mehrere Beobachtungen steht, kann einer Fussnote des Diagramms entnommen werden). Sie geben die beobachteten Werte der Variable Aktienkauf wieder („Y“ steht für 1 und „N“ für 0). Die Zeile unter dem Diagramm (die x-Achse) zeigt die vorhergesagten Wahrscheinlichkeiten und gleich darunter findet sich die darauf basierende Klassifizierung („N“, wenn die Wahrscheinlichkeit < .500 ist, und „Y“, wenn die Wahrscheinlichkeit grösser als .500 ist). Im Idealfall ist die Vorhersage von y nicht nur korrekt, sondern auch möglichst klar – das heisst, wenige Personen weisen mittlere Wahrscheinlichkeiten auf.
Alle „Y“ in der linken Hälfte und alle „N“ in der rechten Hälfte des Diagramms entsprechen somit falschen Vorhersagen. Würden diese gezählt und mit dem Faktor 2.5 (siehe Anmerkung unten in Abbildung 9) multipliziert, so sollten 32 N und 135 Y in der „falschen“ Hälfte gefunden werden. Auch dieses Diagramm zeigt, dass Aktienkauf = 1 eher schlecht vorhergesagt wird.
3.7. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel beträgt R-Quadrat 0.24, doch es stellt sich die Frage, ob dies hoch genug ist, um als bedeutend eingestuft zu werden.
Es gibt verschiedene Arten die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Der Korrelationskoeffizient eignet sich sehr gut, da die Effektstärke dabei immer zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Wenn sich jedoch die Gruppen hinsichtlich ihrer Grösse stark unterscheiden, wird empfohlen, d von Cohen zu wählen, da r durch die Grössenunterschiede verzerrt werden kann.
Das R-Quadrat, das bei Regressionsanalysen ausgegeben wird, kann in eine Effektstärke f nach Cohen (1992) umgerechnet werden. In diesem Fall ist der Wertebereich der Effektstärke zwischen 0 und unendlich.
Um zu beurteilen, wie gross dieser Effekt ist, kann man sich an der Einteilung von Cohen (1988) orientieren:
f2 = .02 entspricht einem schwachen Effekt
f2 = .15 entspricht einem mittleren Effekt
f2 = .35 entspricht einem starken Effekt
Damit entspricht die Effektstärke von .32 einem mittleren Effekt.
3.8. Eine typische Aussage
Eine logistische Regressionsanalyse zeigt, dass sowohl das Modell als Ganzes (Chi-Quadrat(3) = 125.36, p < .001, n = 700) als auch die einzelnen Koeffizienten der Variablen signifikant sind. Steigen das Interesse an der Marktlage sowie die Risikobereitschaft um jeweils eine Einheit, so nimmt die relative Wahrscheinlichkeit eines Aktienkaufs um 8.9% beziehungsweise 41.6% zu. Steigt das Einkommen um 1’000 Franken, so sinkt die relative Wahrscheinlichkeit eines Aktienkaufs um 2.1%. Cohens f2 beträgt .32, was nach Cohen (1992) einem mittleren Effekt entspricht.