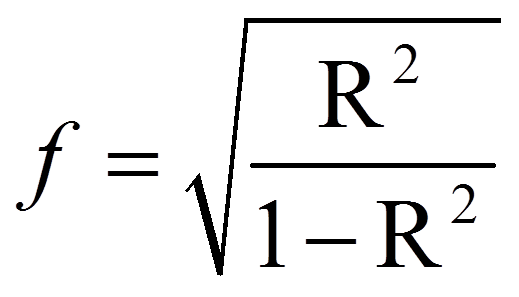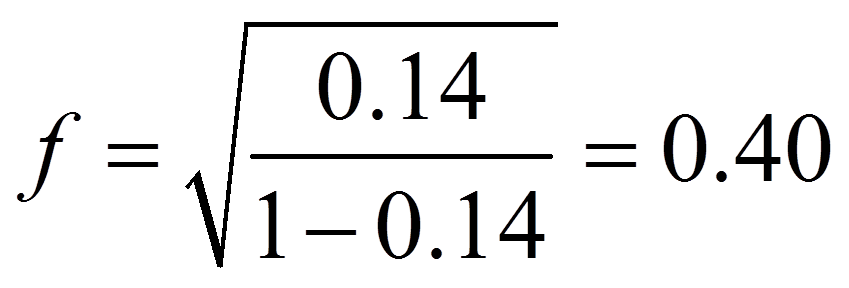 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen der einfachen Regressionsanalyse
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2 Die Methode der kleinsten Quadrate (OLS)
3. Einfache Regressionsanalyse mit SPSS
3.1. Formulierung des Regressionsmodells
3.2. SPSS-Befehle
3.3. Prüfen der Voraussetzungen
3.4. Signifikanz des Regressionsmodells
3.5. Signifikanz der Regressionskoeffizienten
3.6. Modellgüte
3.7. Berechnung der Effektstärke
3.8. Eine typische Aussage
Quick Start
| Wozu wird die einfache Regressionsanalyse verwendet? Um zu prüfen, ob ein Zusammenhang zwischen einer unabhängigen und einer abhängigen Variable besteht. SPSS-Menü
Analysieren > Regression > Linear SPSS-Syntax
REGRESSION /DESCRIPTIVES MEAN STDDEV CORR SIG N /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN /DEPENDENT= abhängige Variable /METHOD=ENTER= unabhängige Variable /SCATTERPLOT=(*ZRESID ,*ZPRED) /RESIDUALS HISTOGRAM(ZRESID). SPSS-Beispieldatensatz
Einfache Regression |
1. Einführung
Die einfache Regressionsanalyse wird auch als „bivariate Regression“ bezeichnet. Sie wird angewandt, wenn geprüft werden soll, ob ein Zusammenhang zwischen zwei intervallskalierten Variablen besteht. „Regressieren“ steht für das Zurückgehen von der abhängigen Variable y auf die unabhängige Variable x. Daher wird auch von „Regression von y auf x“ gesprochen. Die abhängige Variable wird im Kontext der Regressionsanalysen auch als „Kritieriumsvariable“ und die unabhängige Variable als „Prädiktorvariable“ bezeichnet.
Mittels der einfachen Regressionsanalyse können drei Arten von Fragestellungen untersucht werden:
- Ursachenanalyse: Gibt es einen Zusammenhang zwischen der unabhängigen und der abhängigen Variable? Wie eng ist dieser?
- Wirkungsanalyse: Wie verändert sich die abhängige Variable bei einer Änderung der unabhängigen Variablen?
- Prognose: Können die Messwerte der abhängigen Variable durch die Werte der unabhängigen Variable vorhergesagt werden?
Es ist an dieser Stelle anzumerken, dass jeder postulierte Kausalzusammenhang theoretisch begründet sein muss.
Die Fragestellung der Regressionsanalyse wird oft so verkürzt: „Wie beeinflusst eine unabhängige Variablen die abhängige Variable?“ oder „Können die Messwerte der abhängigen Variable durch die Werte der unabhängigen Variablen vorhergesagt werden?“ oder „Wie stark ist der Einfluss der unabhängigen Variable auf die abhängige Variable?“
1.1. Beispiele für mögliche Fragestellungen
- Wie hängen die Körpergrösse und das Volumen des Gehirns zusammen?
- Lässt sich der Anstieg des Umsatzes in Likörläden in den 1950er-Jahren durch den Anstieg der Arbeitslosigkeit beschreiben?
- Um wieviel Franken verändert sich das Monatseinkommen, wenn die wöchentliche Arbeitszeit um eine Stunde steigt?
- Wie hoch sind die prognostizierten Kosten einer Blinddarmresektion?
1.2. Voraussetzungen der einfachen Regressionsanalyse
| ✓ | Die abhängige und die unabhängige Variable sind intervallskaliert. |
| ✓ | Linearität des Zusammenhangs: Es wird ein linearer Zusammenhang zwischen der abhängigen und der unabhängigen Variablen modelliert. |
| ✓ | Linearität der Koeffizienten (Gauss-Markov-Annahme 1): Die Regressionskoeffizienten sind linear. |
| ✓ | Zufallsstichprobe (Gauss-Markov-Annahme 2). |
| ✓ | Bedingter Erwartungswert (Gauss-Markov-Annahme 3): Für jeden Wert der unabhängigen Variablen hat der Fehlerwert den Erwartungswert 0. |
| ✓ | Stichprobenvariation der unabhängigen Variablen (Gauss-Markov-Annahme 4): Die Ausprägungen der unabhängigen Variablen sind nicht konstant. |
| ✓ | Homoskedastizität (Gauss-Markov-Annahme 5): Für jeden Wert der unabhängigen Variablen hat der Fehlerwert dieselbe Varianz. |
| ✓ | Unabhängigkeit des Fehlerwerts: Die Fehlerwerte hängen nicht voneinander ab. |
| ✓ | Normalverteilung des Fehlerwerts: Die Fehlerwerte sind näherungsweise normalverteilt. |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
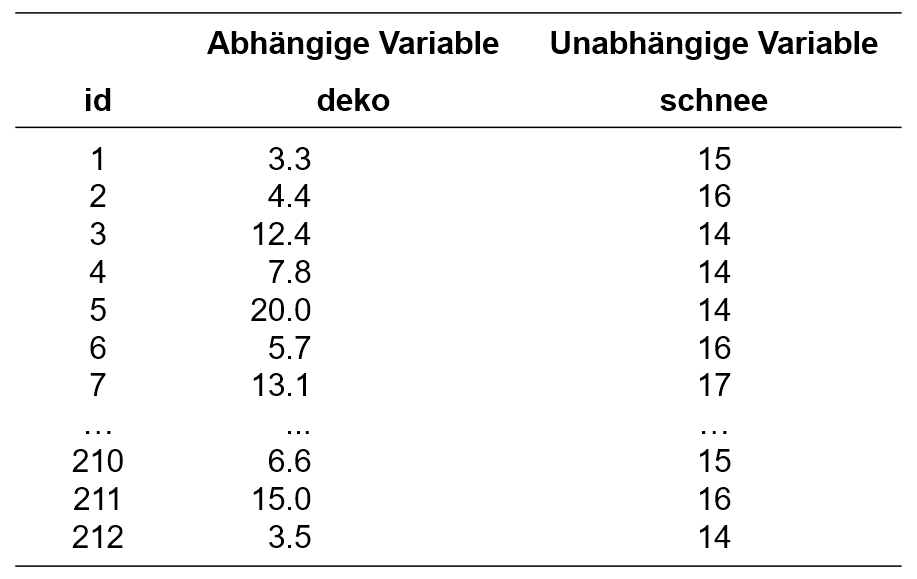
Viele Menschen behaupten, dass bei ihnen erst der erste Schneefall Weihnachtsgefühle weckt. Eine Forschungsgruppe möchte untersuchen, ob Schneefall tatsächlich die Weihnachtsstimmung steigert. Eine bereits veröffentlichte Studie konnte zeigen, dass die Weihnachtsstimmung durch die Anzahl gekaufter Weihnachtsdekorationsartikel operationalisiert werden kann. Die Forschungsgruppe formuliert nun die folgende Forschungsfrage: Besteht ein Zusammenhang zwischen der Anzahl schneefallreicher Tage in der Vorweihnachtszeit und dem Umsatz (in Tausend Schweizer Franken) in Dekorationsgeschäften (n = 212)?
Der zu analysierende Datensatz enthält daher neben einer Identifikationsnummer des Dekorationsgeschäfts (id) eine Variable, die den Umsatz erfasst (deko), und eine, die die Anzahl Tage mit Schneefall wiedergibt (schnee).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2 Die Methode der kleinsten Quadrate (OLS)
Die Regressionsanalyse beruht auf der Grundidee, einen Zusammenhang zwischen Variablen durch eine lineare Funktion zu beschreiben (mathematisch: eine Gerade). Die abhängige Variable y wird als Funktion der unabhängigen Variablen xi beschrieben: y = f(xi).
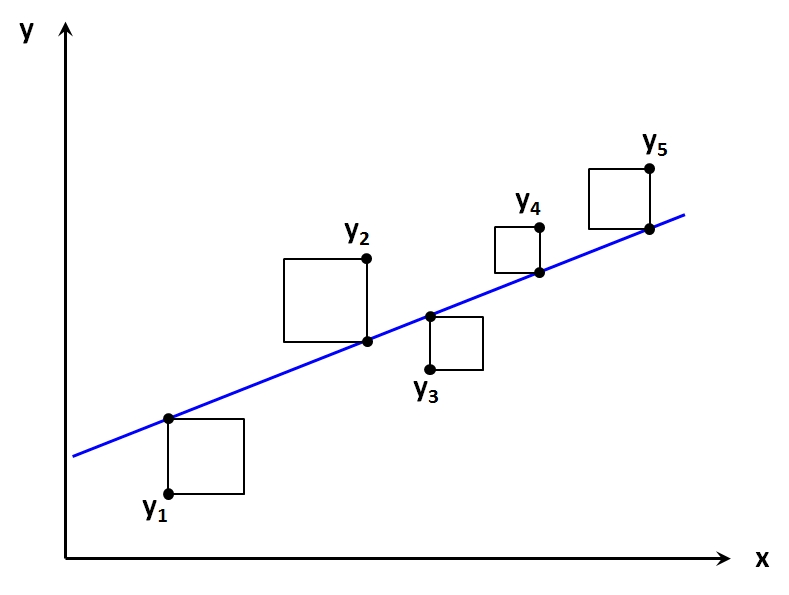
Im Fall von lediglich einer unabhängigen Variable lässt sich dies graphisch veranschaulichen: Die abhängige Variable wird auf der Y-Achse abgetragen, die unabhängige auf der X-Achse. Abbildung 2 zeigt ein so entstandenes Streudiagramm mit fünf beobachteten Werten (mit y1 bis y5 beschriftete Punkte). Die Regressionsgerade (blau in Abbildung 2) wird nun möglichst optimal durch die „Punktwolke“ gelegt.
„Optimal“ bedeutet in diesem Kontext, dass die Summe der quadrierten vertikalen Abstände von den beobachteten Werten zur Regressionsgerade minimiert wird. Dies ist die Summe der quadratischen Flächen in Abbildung 2. Daher stammt auch der Name dieser Berechnungsmethode: „Methode der kleinsten Quadrate“ (auch „OLS-Methode“, denn engl.: Ordinary Least Square Method).
Das Quadrieren hat einerseits zur Folge, dass sich positive und negative Abstände von den Datenpunkten zur Geraden nicht gegenseitig aufheben, und andererseits fliessen so grössere Abstände mit einem höheren Gewicht in die Berechnung ein.
Das Regressionsmodell
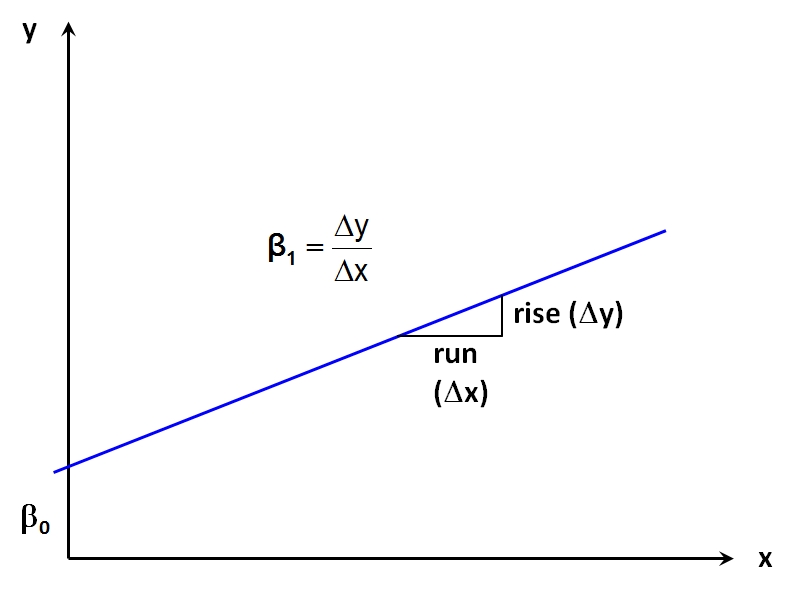
Die Regressionsgerade wird – wie jede Gerade – durch einen y-Achsenabschnitt und ihre Steigung charakterisiert. Im Kontext der bivariaten Regressionsanalyse wird der y-Achsenabschnitt als β0 („Beta Null“, in SPSS auch „Konstante“) bezeichnet. Er entspricht dem Wert der abhängigen Variablen y, wenn x Null beträgt. Die Steigung wird als β1 („Beta Eins“) bezeichnet. Sie beschreibt die Veränderung der abhängigen Variable y, wenn die unabhängige Variable x um eine Einheit ansteigt (engl. „the rise over the run“). Je nach Vorzeichen von β1 ist diese Veränderung eine Zunahme oder eine Abnahme. Abbildung 3 illustriert dies. β0 und β1 werden als „Regressionskoeffizienten“ bezeichnet.
Da die beobachteten Werte in der Regel nicht auf der Regressionsgeraden liegen (vgl. Abbildung 2), beinhaltet ein Regressionsmodell immer auch einen Fehlerwert (Fehlerterm ε), der eben diesen Unterschieden zwischen Modell und Daten Rechnung trägt. Er stellt die Einflüsse auf die abhängige Variable dar, welche nicht auf die unabhängige Variable zurückzuführen sind. Anders ausgedrückt ist der Fehlerwert der Unterschied zwischen dem durch die Regressionsgerade vorhergesagten Wert des Probanden i und dem tatsächlich gemessenen Wert des Probanden i.
Dies ergibt das folgende Regressionsmodell:
mit
| = | Wert der abhängigen Variable des Probanden i | |
| = | Wert der unabhängigen Variable des Probanden i | |
| = | Fehlerterm des Probanden i | |
| = | Regressionskoeffizienten |
Die Berechnung der Regressionskoeffizienten basiert auf einer Stichprobe, weswegen Schätzungen für die Populationsparameter β0 und β1 vorgenommen werden müssen: β ̂_0 und β ̂_1 („Beta Null Dach“ und „Beta Eins Dach“). Da jedoch bei Regressionsanalysen stets Schätzungen von Populationsparametern anhand einer Stichprobe vorgenommen werden (da es kaum je möglich ist, die Gesamtpopulation zu untersuchen), wird das „Dach“ oftmals weggelassen.
3. Einfache Regressionsanalyse mit SPSS
3.1. Formulierung des Regressionsmodells
Im Falle des vorliegenden Beispiels stellt deko die abhängige Variable dar, die auf die unabhängige Variable schnee regressiert wird. Daher wird das folgende Modell postuliert:
Hinweis
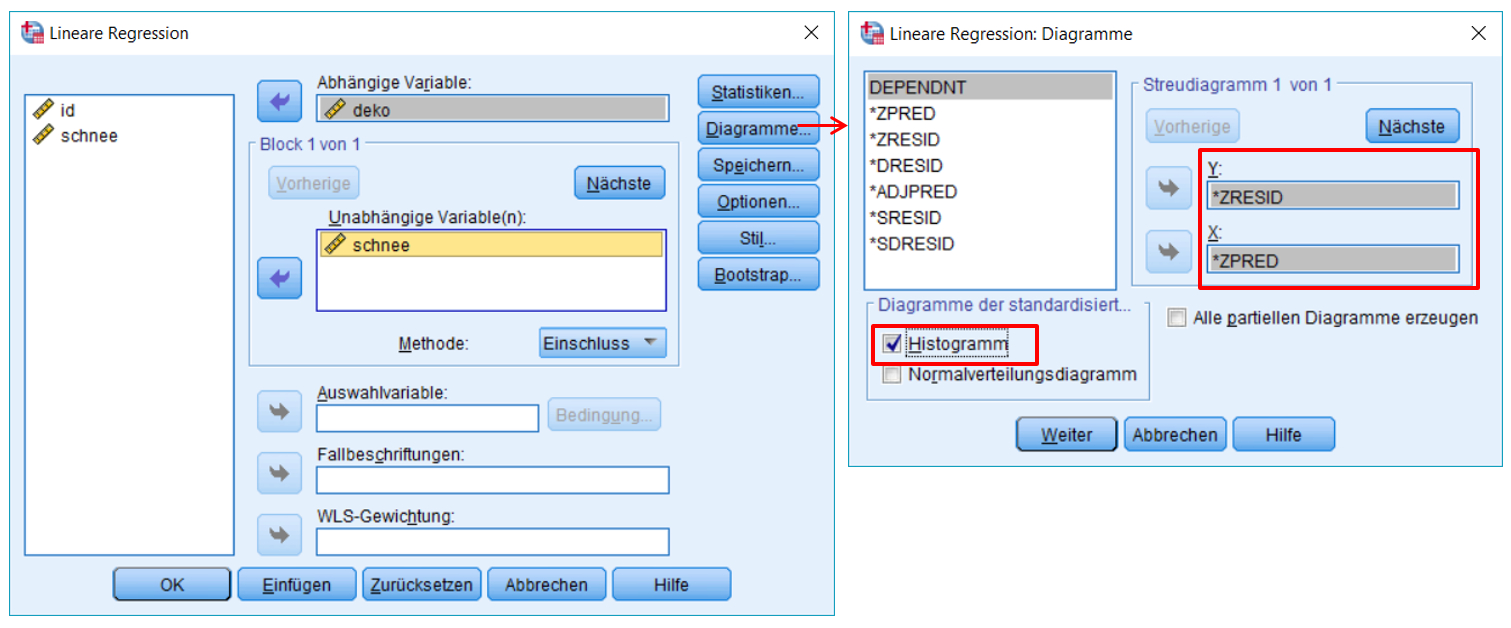
- Unter Diagramme kann ein Streudiagramm zur Prüfung der Homoskedastizität erstellt werden. Dazu wird ZRESID auf der Y-Achse und ZPRED auf der X-Achse abgetragen. Zudem kann ein Histogramm der standardisierten Residuen angefordert werden.
SPSS-Syntax
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGI
/DEPENDENT deko
/METHOD=ENTER schnee
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
3.3. Prüfen der Voraussetzungen
Bevor die Resultate der Regressionsanalyse analysiert werden, sollen Voraussetzungen geprüft werden. Dies sind die Linearität des Zusammenhangs, die Gauss-Markov-Annahmen sowie die Annahmen zur Unabhängigkeit und die Normalverteilung der Fehlerwerte.
Linearität des Zusammenhangs
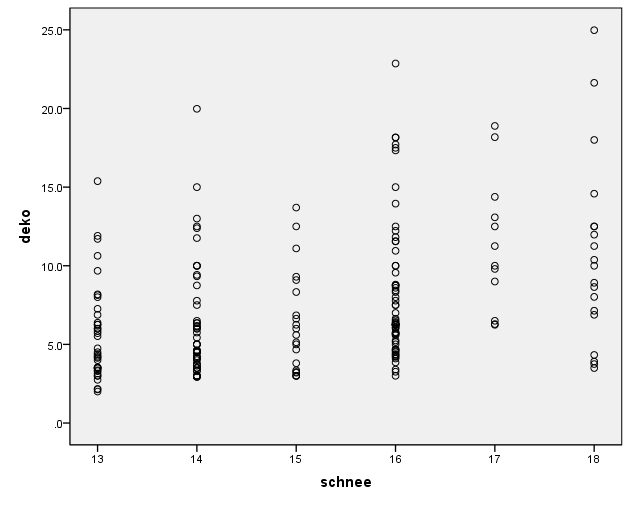
Es wurde ein lineares Modell postuliert. Um visuell zu prüfen, ob dies haltbar ist, wird ein Streudiagramm (ein „Scatterplot“) zwischen der abhängigen und der unabhängigen Variable erstellt (siehe Abbildung 5). Dieses kann über das SPSS-Menü:
Grafik > Diagrammerstellung > Streu-/Punktdiagramm > Einfaches Streudiagramm erstellt werden.
Das Streudiagramm lässt für das Beispiel einen nicht sehr engen, positiven Zusammenhang vermuten. Damit scheint die Voraussetzung, dass der Zusammenhang an sich linear ist, erfüllt.
Es gilt anzumerken, dass auch nicht-lineare Zusammenhänge zwischen y und x mittels Regressionsanalyse untersucht werden können. Dazu wird der Zusammenhang vor der Regressionsanalyse derart transformiert, dass er linear wird. Dies geschieht durch eine Transformation von y und/oder x. Anschliessend wird nicht der Zusammenhang zwischen y und x modelliert, sondern zwischen den allenfalls transformierten Variablen.
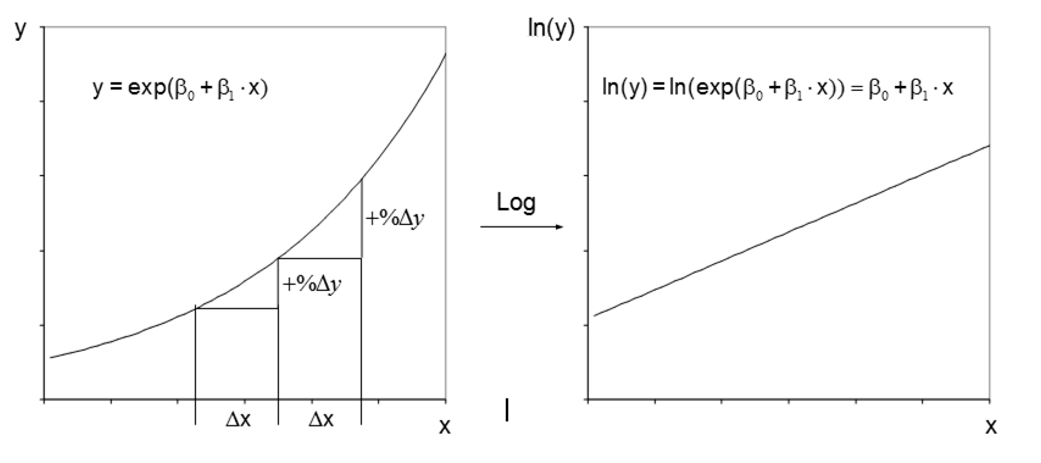
Ist beispielsweise der prozentuale Anstieg von y konstant, wenn x um eine Einheit erhöht wird, so ist eine Logarithmierung von y angemessen, wie Abbildung 6 verdeutlicht. Während der Zusammenhang zwischen y und x nicht linear ist, ist jener zwischen der transformierten Variable ln(y) und x linear.
Weitere Transformationen sind möglich; so kann beispielsweise auch x quadriert oder logarithmiert werden oder es könnte die Wurzel von x verwendet werden. Abschliessend soll festgehalten werden: Nicht-lineare Variablen sind möglich und oft sehr nützlich. Davon zu unterscheiden ist die Voraussetzung der Linearität der Koeffizienten, die zwingend erfüllt sein muss.
Linearität der Koeffizienten (Gauss-Markov-Annahme 1)
Das postulierte Modell ist linear in den Koeffizienten:
Zufällige Stichprobe (Gauss-Markov-Annahme 2)
Die Antwort auf die Frage, ob diese Voraussetzung erfüllt ist, wird auf der Basis von Hintergrundwissen zum Datensatz gefunden. Für das Beispiel wird davon ausgegangen, dass die Forschenden eine zufällige Stichprobe gezogen haben.
Bedingter Erwartungswert (Gauss-Markov-Annahme 3)
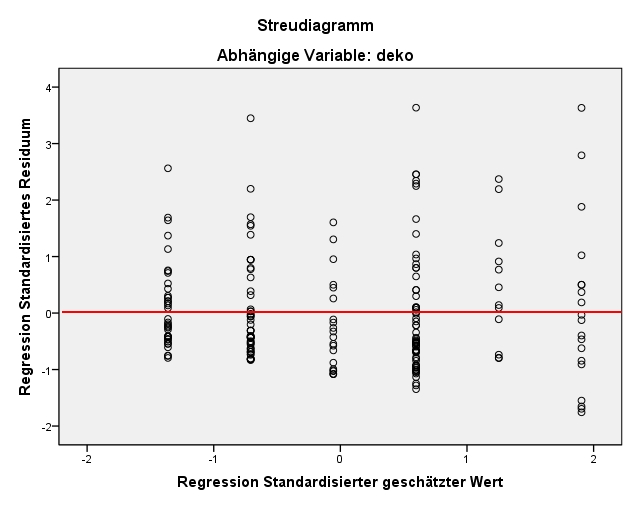
Diese Voraussetzung verlangt, dass der Fehlerwert ε für jeden Wert der unabhängigen Variablen den Erwartungswert 0 hat. Zur Prüfung dieser Annahme wird ein Streudiagramm der standardisierten, geschätzten Werte von y (auf der x-Achse) und der standardisierten Fehlerwerte (Residuen; auf der y-Achse) erzeugt. Es wird anschliessend visuell geprüft, ob über den gesamten Wertebereich der geschätzten Werte der Fehler im Mittel 0 beträgt.
Wie in Abbildung 7 zu erkennen ist, ist es möglich, dass der Mittelwert der Fehlerwerte ungefähr bei 0 liegt: Die negativen und die positiven Abweichungen von 0 auf der y-Achse („gegen oben“ und „gegen unten“) gleichen sich im Mittel etwa aus.
Stichprobenvariation der unabhängigen Variablen (Gauss-Markov-Annahme 4)
Wie das Streudiagramm von deko und schnee in Abbildung 5 bereits gezeigt hat, ist die unabhängige Variable schnee nicht konstant, sondern sie weist Varianz auf.
Homoskedastizität (Gauss-Markov-Annahme 5)
Homoskedastizität bedeutet, dass der Fehler für jeden Wert der unabhängigen Variablen die gleiche Varianz aufweist. Geprüft wird diese Voraussetzung oft im gleichen Streudiagramm, in welchem bereits der bedingte Erwartungswert des Fehlers geprüft wurde. Es wird visuell geprüft, ob über den gesamten Wertebereich der geschätzten Werte der Fehler die gleiche Varianz aufweist. Dies scheint im vorliegenden Beispiel der Fall zu sein (siehe Abbildung 7). Das heisst, es liegt vermutlich Homoskedastizität vor.
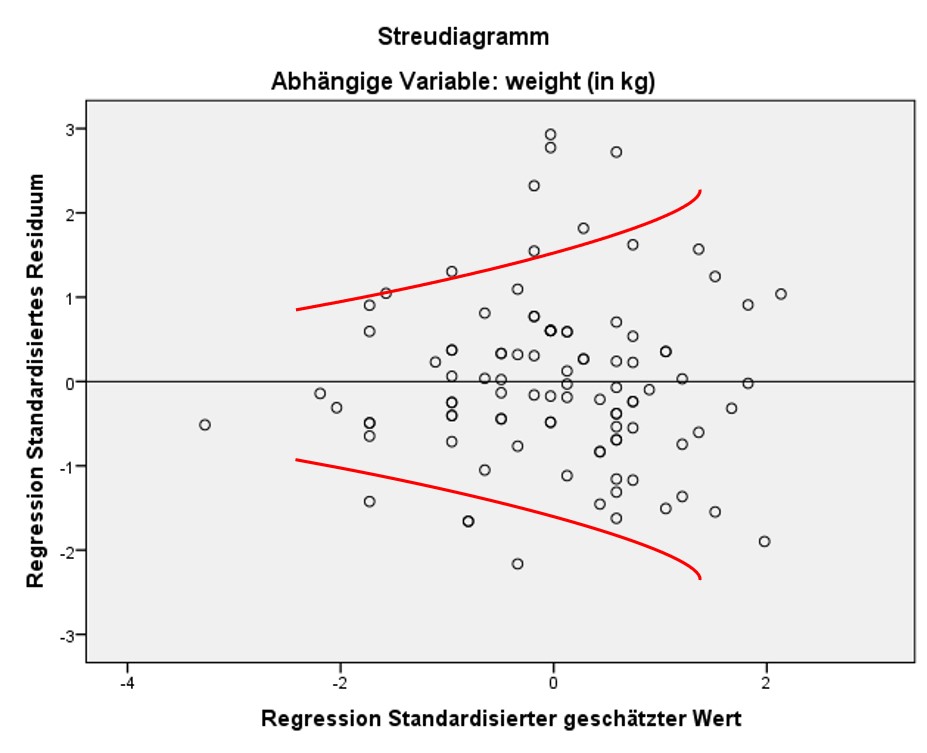
Liegt keine Homoskedastizität vor, der Fehler hat also nicht über den ganzen Wertebereich der geschätzten Werte die gleiche Varianz, so wird von Heteroskedastizität gesprochen. Dies ist daran zu erkennen, dass das Streudiagramm ein eindeutiges Muster aufweist, wie beispielsweise eine Trompetenform (wie in Abbildung 8 dargestellt).
Neben der visuellen Inspektion liegen auch statistische Tests zur Überprüfung dieser Voraussetzung vor, welche jedoch in SPSS derzeit nicht implementiert sind. Dies sind beispielsweise der Breusch-Pagan-Test / Cook-Weisberg-Test und der White-Test. Abhilfe bei Heteroskedastizität kann beispielsweise eine Transformation einer Variable bringen oder es können robuste Standardfehler verwendet werden (in SPSS nicht implementiert).
Unabhängigkeit des Fehlerwerts
Diese Annahme verlangt, dass die Fehlerterme verschiedener Beobachtungen (hier: Verkaufsstellen) nicht zusammenhängen, also keinen Einfluss aufeinander haben. Auch zur Prüfung dieser Annahme wird auf das Streudiagramm in Abbildung 7 zurückgegriffen. Sind die Fehler voneinander unabhängig, so sollte sich kein Muster zeigen, wie beispielsweise ein wellenförmiger Verlauf. Eine Verletzung dieser Voraussetzung tritt meistens nur dann auf, wenn Zeitreihendaten, geclusterte Beobachtungen (e.g. mehrere Beobachtungen in der gleichen Schulklassen, dem gleichen Haushalt, dem gleichen Wahlbezirk etc.) oder Paneldaten vorliegen (e.g. gleiche Personen mehrfach befragt).
Im vorliegenden Beispiel gibt es keinen Hinweis auf ein Problem, so dass von unkorrelierten Fehlern ausgegangen wird.
Neben der visuellen Inspektion stellt SPSS auch statistische Tests zur Überprüfung dieser Voraussetzung zur Verfügung: den Durbin-Watson-Test. Dieser wird beim Beispiel zur multiplen Regression verwendet und kommentiert.
Normalverteilung des Fehlerwerts
Die Residuen sollten näherungsweise normalverteilt sein. Dies wird in der Regel anhand eines Histogramms der standardisierten Residuen visuell beurteilt. Abbildung 9 lässt erkennen, dass die Verteilung des Residuums in den Beispieldaten rechtsschief ist.
Da nun alle Voraussetzungen geprüft worden sind und – zwar nicht ideal jedoch akzeptabel – erfüllt sind, werden das Regressionsmodell als Ganzes und die einzelnen Regressionskoeffizienten auf statistische Signifikanz geprüft.
3.4. Signifikanz des Regressionsmodells
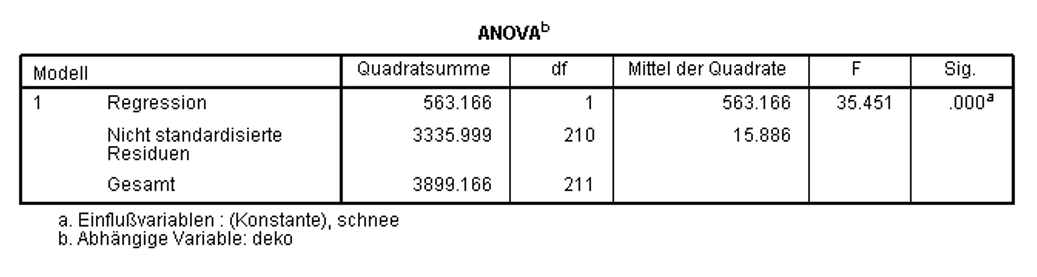
Zur Überprüfung, ob das Regressionsmodell insgesamt signifikant ist, wird ein F-Test durchgeführt. Dieser prüft, ob die Vorhersage der abhängigen Variablen durch das Hinzufügen der unabhängigen Variablen verbessert wird. Das heisst, der F-Test prüft, ob das Modell insgesamt einen Erklärungsbeitrag leistet.
In Abbildung 10 ist zu erkennen, dass das Modell als Ganzes signifikant ist (F(1,210) = 35.451, p < .001). Aus diesem Grund wird die Analyse fortgesetzt. Wäre das Modell als Ganzes nicht signifikant, so würde die Analyse nicht fortgesetzt.
3.5. Signifikanz der Regressionskoeffizienten
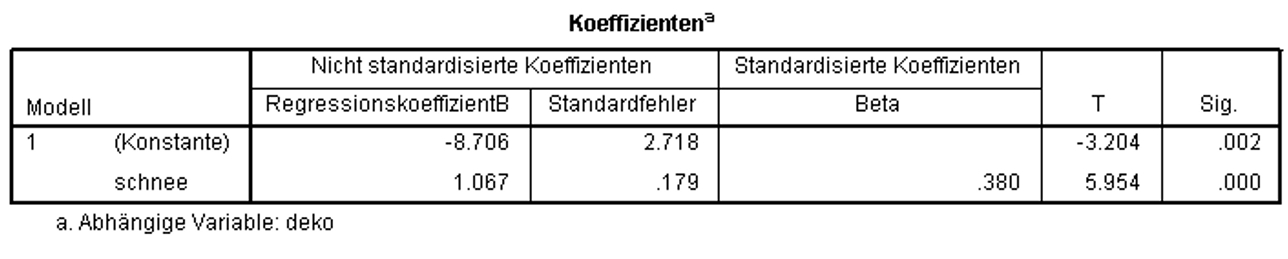
Nun wird geprüft, ob die Regressionskoeffizienten (Betas) ebenfalls signifikant sind. Dabei wird für jeden der Regressionskoeffizienten ein t-Test durchgeführt. Die Ergebnisse des t–Tests können den Spalten „T“ und „Sig.“ in Abbildung 11 entnommen werden.
Abbildung 11 zeigt, dass die t-Tests für den Regressionskoeffizienten von schnee (t = 5.954, p < .001) und die Konstante (d.h. der Y-Achsenabschnitt; t = -3.204, p = .002) signifikant ausfallen. Eine signifikante Konstante bedeutet, dass der Y-Achsenabschnitt nicht 0 beträgt und damit die Regressionsgerade nicht durch den Ursprung geht. Der signifikante Koeffizient von schnee bedeutet, dass der Regressionskoeffizient von schnee nicht 0 ist und schnee somit einen signifikanten Einfluss auf deko aufweist. Somit ergibt sich folgende Regressionsgerade:
3.6. Modellgüte
Das sogenannte R2 wird auch als „Bestimmtheitsmass“ bezeichnet. Es zeigt, wie gut das geschätzte Modell zu den erhobenen Daten passt. R2 beschreibt, welcher Anteil der Gesamtstreuung in der abhängigen Variable durch die unabhängige Variable erklärt werden kann. R2 kann Werte zwischen 0 und 1 annehmen. 0 bedeutet, dass das Modell keine Erklärungskraft besitzt, 1 bedeutet, dass das Modell die beobachteten Werte perfekt vorhersagen kann. Je höher der R2-Wert, desto besser also die Passung zwischen Modell und Daten (daher engl. „Goodness of fit“).
R2 wird von der Anzahl der unabhängigen Variablen im Modell beeinflusst. Dies ist im Falle der multiplen Regression problematisch, da mehrere unabhängige Variablen in das Modell einbezogen werden. Hier steigt das R2 mit der Anzahl der unabhängigen Variablen, auch wenn die zusätzlichen Variablen keinen Erklärungswert haben. Daher wird R2 nach unten korrigiert („Korrigiertes R2„). Diese Korrektur fällt umso grösser aus, je mehr Variablen im Modell sind und umso kleiner, je grösser die Stichprobe ist. Der SPSS-Output enthält immer R2 und das korrigierte R2 (siehe Abbildung 12). Auch im Falle der einfachen Regression, wo nur eine unabhängige Variable im Modell ist, wird in der Regel das korrigierte R2 berichtet.
Im vorliegenden Beispiel beträgt das korrigierte R2 .140, was bedeutet, dass 14.0% der Gesamtstreuung in deko durch schnee erklärt werden kann (Abbildung 12).
3.7. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel wird 14.0% der Gesamtstreuung in der abhängigen Variable durch die unabhängige Variable erklärt, doch es stellt sich die Frage, ob dies hoch genug ist, um als bedeutend eingestuft zu werden.
Das R2, das bei Regressionsanalysen ausgegeben wird, kann in eine Effektstärke f nach Cohen (1992) umgerechnet werden. In diesem Fall ist der Wertebereich der Effektstärke zwischen 0 und unendlich.
3.8. Eine typische Aussage
Die Anzahl schneereicher Tage (schnee) hat einen Einfluss darauf, wie viel Weihnachtsdekoration (deko) verkauft wird (F(1, 210) = 35.451, p < .001). Mit einem Tag mehr Schnee steigt der Umsatz an Weihnachtsdekoration um 1’067 Schweizer Franken. 14.0% der Streuung des Umsatzes an Weihnachtsdekoration wird durch die Anzahl schneereicher Tage erklärt, was nach Cohen (1992) einem starken Effekt entspricht.