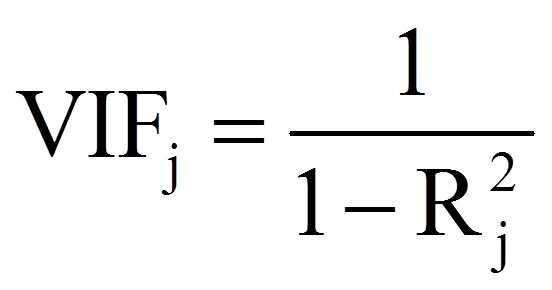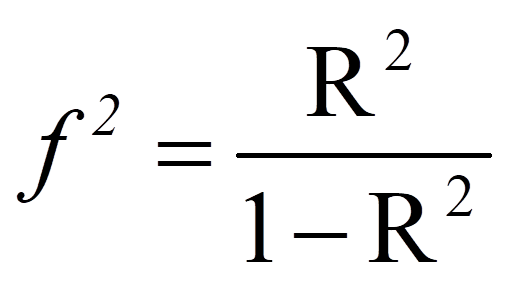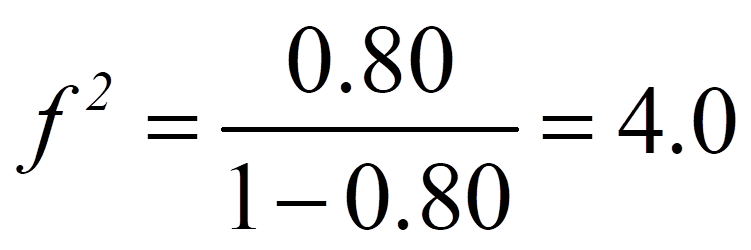 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen der multiplen Regressionsanalyse
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Methode der kleinsten Quadrate (OLS)
3. Multiple Regressionsanalyse mit SPSS
3.1. Formulierung des Regressionsmodells
3.2. Methoden des Variableneinschlusses
3.3. SPSS-Befehle
3.4. Prüfen der Voraussetzungen
3.5. Signifikanz des Regressionsmodells
3.6. Signifikanz der Regressionskoeffizienten
3.7. Modellgüte
3.8. Berechnung der Effektstärke
3.9. Eine typische Aussage
Quick Start
| Wozu wird die multiple Regressionsanalyse verwendet? Die multiple Regressionsanalyse testet, ob ein Zusammenhang zwischen mehreren unabhängigen und einer abhängigen Variable besteht. SPSS-Menü
Analysieren > Regression > Linear SPSS-Syntax
REGRESSION /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA COLLIN TOL /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN /DEPENDENT abhängige Variable /METHOD=ENTER unabhängige Variablen /PARTIALPLOT ALL /SCATTERPLOT=(*ZRESID ,*ZPRED) /RESIDUALS DURBIN HISTOGRAM(ZRESID). SPSS-Beispieldatensatz
Multiple Regression |
1. Einführung
Die multiple Regressionsanalyse testet, ob ein Zusammenhang zwischen mehreren unabhängigen und einer abhängigen Variable besteht.
„Regressieren“ steht für das Zurückgehen von der abhängigen Variable y auf die unabhängigen Variablen xk. Daher wird auch von „Regression von y auf x“ gesprochen. Die abhängige Variable wird im Kontext der Regressionsanalysen auch als „Kritieriumsvariable“ und die unabhängigen Variablen als „Prädiktorvariablen“ bezeichnet.
In der empirischen Sozialforschung sowie in der Marktforschung gibt es selten nur eine Ursache für eine Wirkung. In der Regel werden die Werte einer abhängigen Variablen durch mehrere unabhängige Variablen beeinflusst. Diesem Umstand kann durch die multiple Regressionsanalyse Rechnung getragen werden. Sie ist eine Erweiterung der einfachen Regression und ermöglicht es, mehrere unabhängige Variablen gleichzeitig in einem Modell zu berücksichtigen.
Das Konzept und die Vorgehensweise basieren auf der einfachen Regression. Es müssen jedoch zusätzliche Voraussetzungen beachtet werden. Des Weiteren gibt es bei der multiplen Regression im Unterschied zur einfachen Regression verschiedene Arten, die unabhängigen Variablen in das Modell einzubeziehen (siehe Multiple Regression mit SPSS).
Mittels der einfachen Regressionsanalyse können drei Arten von Fragestellungen untersucht werden:
- Ursachenanalyse: Gibt es einen Zusammenhang zwischen der unabhängigen und der abhängigen Variable? Wie eng ist dieser?
- Wirkungsanalyse: Wie verändert sich die abhängige Variable bei einer Änderung der unabhängigen Variablen?
- Prognose: Können die Messwerte der abhängigen Variable durch die Werte der unabhängigen Variable vorhergesagt werden?
Es ist an dieser Stelle anzumerken, dass jeder postulierte Kausalzusammenhang theoretisch begründet sein muss.
Die Fragestellung der multiplen Regressionsanalyse wird oft so verkürzt:
„Wie beeinflussen mehrere unabhängige Variablen die abhängige Variable?“, oder:
„Können die Messwerte der abhängigen Variable durch die Werte der unabhängigen Variablen vorhergesagt werden?“, oder:
„Wie stark ist der Einfluss jeder unabhängigen Variable auf die abhängige Variable?“
1.1. Beispiele für mögliche Fragestellungen
- Wie beeinflussen die Abschlussnote und die Vorbereitungszeit das Abschneiden bei einem Eignungstests zur Zulassung zum Medizinstudium?
- Wird die Absatzmenge eines Produktes durch den Produktpreis, die Verpackungstyp und den produktspezifischen Werbeaufwand beeinflusst?
- Wie stark wird die Arbeitszufriedenheit durch den Lohn, die wöchentliche Arbeitszeit, die subjektiv wahrgenommenen Ausstiegschancen und die empfundene Wertschätzung beeinflusst?
- Welchen Einfluss haben die Witterung, die Auslastung, die Tageszeit, die Region, das Rollmaterial und der Wochentag auf die Pünktlichkeit von Zügen?
1.2. Voraussetzungen der multiplen Regressionsanalyse
| ✔ | Die abhängige Variable ist intervallskaliert und die unabhängigen Variablen sind intervallskaliert oder als Dummy-Variablen codiert. |
| ✔ | Linearität des Zusammenhangs: Es wird ein linearer Zusammenhang zwischen der abhängigen und den unabhängigen Variablen modelliert |
| ✔ | Linearität der Koeffizienten (Gauss-Markov-Annahme 1): Die Regressionskoeffizienten sind linear. |
| ✔ | Zufallsstichprobe (Gauss-Markov-Annahme 2). |
| ✔ | Bedingter Erwartungswert (Gauss-Markov-Annahme 3): Für jeden Wert der unabhängigen Variablen hat der Fehlerwert den Erwartungswert 0. |
| ✔ | Stichprobenvariation der unabhängigen Variablen (Gauss-Markov-Annahme 4): Die Ausprägungen der unabhängigen Variablen sind nicht konstant. |
| ✔ | Homoskedastizität (Gauss-Markov-Annahme 5): Für jeden Wert der unabhängigen Variablen hat der Fehlerwert dieselbe Varianz. |
| ✔ | Unabhängigkeit des Fehlerwerts: Die Fehlerwerte hängen nicht voneinander ab. |
| ✔ | Normalverteilung des Fehlerwerts: Die Fehlerwerte sind näherungsweise normalverteilt. |
| ✔ | Keine Multikollinearität: Die unabhängigen Variablen korrelieren nicht zu stark miteinander. |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
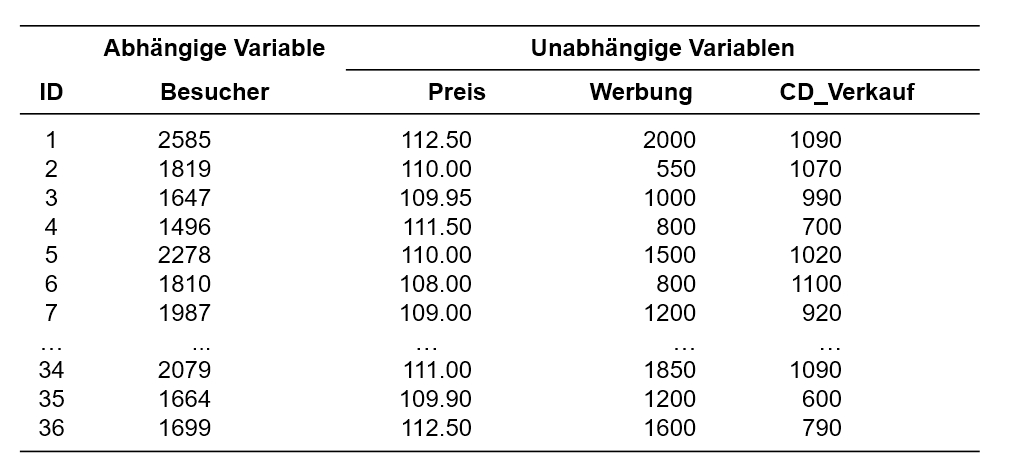
Ein Club organisiert regelmässig Konzerte. Um den Umsatz zu optimieren möchten die Konzertveranstalter herausfinden, welche Faktoren zum Erfolg (Anzahl Besucher) eines Konzertes beitragen. Aus ihrer langjährigen Erfahrung wissen sie, dass der Erfolg unter anderem vom Ticketpreis (in Schweizer Franken), dem Werbeaufwand (in Schweizer Franken), sowie dem Erfolg der Band (Anzahl verkaufter CDs) abhängt. Dies möchte sie nun statistisch überprüfen, um künftig den Erfolg eines Konzertes im Voraus besser abschätzen zu können.
Der zu analysierende Datensatz enthält daher neben einer Identifikationsnummer des Anlasses (ID) die Besucherzahl des Anlasses (Besucher), den Ticketpreis (Preis), den betriebenen Werbeaufwand (Werbung) und die Anzahl verkaufter CDs (CD_Verkauf).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Methode der kleinsten Quadrate (OLS)
Das Grundprinzip der multiplen Regressionsanalyse basiert wie die einfache Regressionsanalyse auf der „Methode der kleinsten Quadrate“ (auch „OLS-Methode“, denn engl.: Ordinary Least Square Method). Im Kapitel zur einfachen Regressionsanalyse findet sich eine sehr kurze Erläuterung.
Das Regressionsmodell
Das Regressionsmodell lässt sich wie bei der einfachen Regression anhand sogenannter „Regressionskoeffizienten“ beschreiben, jedoch wird bei der multiplen Regression für jede unabhängige Variable ein zusätzlicher Regressionskoeffizient hinzugefügt (z.B. β2, β3, etc.), so dass das Modell die folgende Form annimmt:
mit
| = | Schätzer der abhängigen Variable | |
| = | unabhängige Variable k | |
| = | Regressionskoeffizient der Variable xk | |
| = | Fehlerterm des Probanden i |
Die Interpretation der Regressionskoeffizienten folgt dem folgenden Schema: „Wenn xk um eine Einheit steigt, so verändert sich y um βk Einheiten, gegeben alle anderen unabhängigen Variablen werden konstant gehalten.“ Je nach Vorzeichen von βk ist diese Veränderung eine Zunahme oder eine Abnahme.
3. Multiple Regressionsanalyse mit SPSS
3.1. Formulierung des Regressionsmodells
Im Falle des vorliegenden Beispiels stellt Besucher die abhängige Variable dar, die auf die unabhängigen Variablen Preis, Werbung und CD_Verkauf regressiert wird. Daher wird das folgende Modell postuliert:
Bei der Auswahl der Variablen im Modell spielen theoretische Überlegungen eine zentrale Rolle. Das Modell sollte möglichst einfach gehalten werden. Daher empfiehlt es sich, nicht zu viele unabhängige Variablen aufzunehmen.
3.2. Methoden des Variableneinschlusses
Vor der Durchführung der Analyse muss entschieden werden, in welcher Reihenfolge die unabhängigen Variablen in das Modell aufgenommen werden sollen. Dies kann einen Einfluss auf das Modell haben, das am Ende der Analyse berichtet wird. Sind alle unabhängigen Variablen vollständig unkorreliert, so spielt die Reihenfolge, in der sie in das Modell eingeführt werden, keine Rolle. In den Sozialwissenschaften sowie in der Marktforschung sind die Variablen jedoch selten vollständig unkorreliert. Somit ist die Methode des Variableneinschlusses relevant.
Methoden des Variableneinschlusses in SPSS
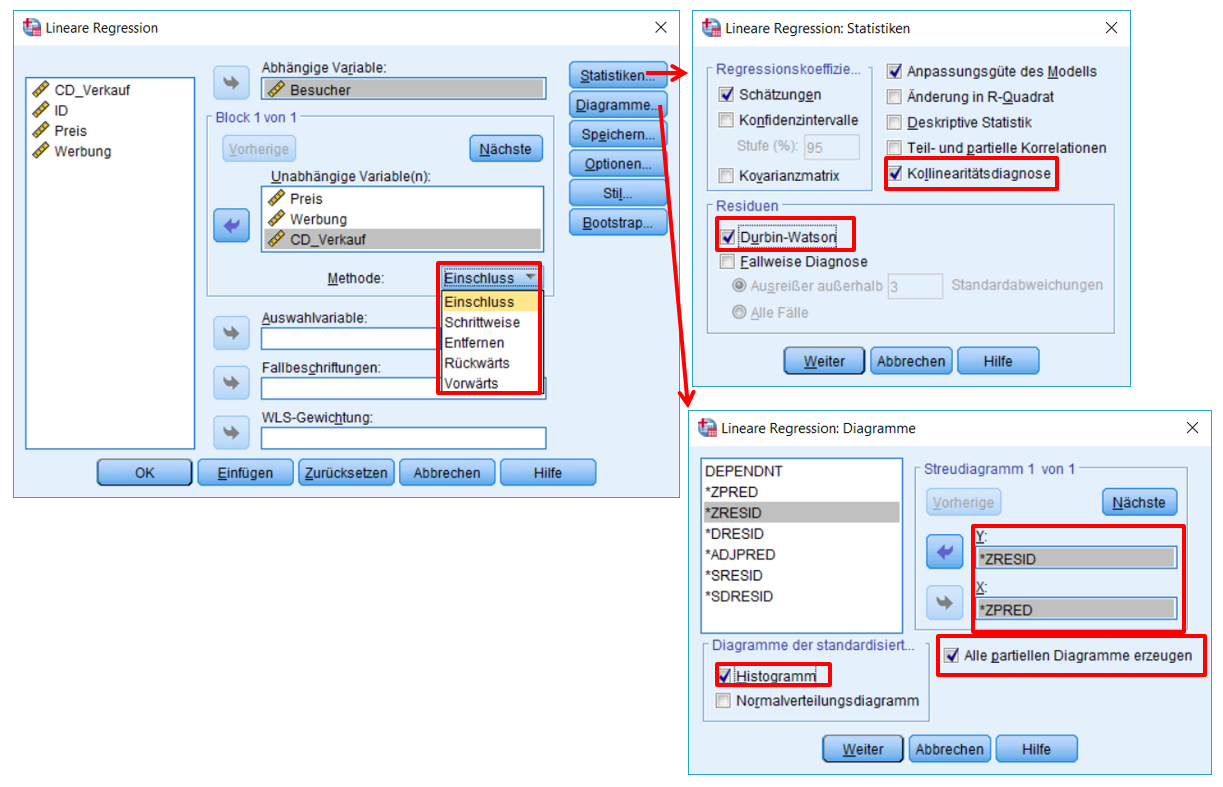
SPSS bietet verschiedene Vorgehensweisen an, um die unabhängigen Variablen in das Modell aufzunehmen (vgl. Klicksequenz in Abbildung 4):
- Einschluss (ENTER): Bei dieser Methode werden alle Variablen gleichzeitig in das Modell eingefügt. Diese Methode wird angewandt, wenn das Modell auf theoretischen Überlegungen basiert. Diese Methode eignet sich also, um Theorien zu testen, während die übrigen Methoden eher im Rahmen explorativer Studien eingesetzt werden.
- Vorwärts-Selektion (FORWARD): Die Variablen werden sequenziell in das Modell aufgenommen. Diejenige unabhängige Variable, welche am stärksten mit der abhängigen Variable korreliert wird zuerst zum Modell hinzugefügt. Dann wird jene der verbleibenden Variablen hinzugefügt, die die höchste partielle Korrelation mit der abhängigen Variablen aufweist. Dieser Schritt wird wiederholt, bis sich die Modellgüte (R-Quadrat) nicht weiter signifikant erhöht oder alle Variablen ins Modellaufgenommen worden sind.
- Rückwärts-Elimination (BACKWARD): Zunächst sind alle Variablen im Regressionsmodell enthalten und werden anschliessend sequenziell entfernt. Schrittweise wird immer diejenige unabhängige Variable entfernt, welche die kleinste partielle Korrelation mit der abhängigen Variable aufweist, bis entweder keine Variablen mehr im Modell sind oder keine die verwendeten Ausschlusskriterien erfüllen.
- Schrittweise (STEPWISE): Diese Methode ist ähnlich wie „Vorwärts“-Selektion, es wird aber zusätzlich bei jedem Schritt getestet, ob die am wenigsten „nützliche“ Variable entfernt werden soll.
Im vorliegenden Beispiel beruht das Regressionsmodell auf fundierten theoretischen Überlegungen, weswegen die „Einschluss“-Methode gewählt wird.
Hierarchische Regressionsanalyse
Zusätzlich können Variablen auch in Blöcken eingeführt werden (daher engl. auch „blockwise regression“). Dies ist den bisher beschriebenen Vorgehensweisen übergeordnet und kann beliebig mit diesen kombiniert werden. Dabei werden mehrere Variablengruppen (Blöcke) vorgegeben, die SPSS nacheinander in das Modell aufnimmt. Innerhalb von jedem Block wird die bereits gewählte Methode angewendet (z.B. „Einschluss“ oder „Schrittweise“). In einer Studie zum Einfluss des Umweltbewusstseins auf das Verhalten könnte beispielsweise mit dem ersten Block ein Modell gebildet werden, das soziodemographischen Variablen beinhaltet. Im zweiten Block wird dann das Umweltbewusstsein eingeführt. In SPSS werden dabei nicht alle Variablen gleichzeitig in die Box „Unabhängige“ eingetragen, sondern lediglich jene des ersten Blocks. Dann wird „Weiter“ gewählt und die Variablen des zweiten Blocks werden eingefügt, etc.
Dieses Vorgehen hat zwei Vorteile: Erstens kann auf diese Weise die Reihenfolge des Variableneinschlusses genau vorgegeben werden. Zweitens gibt SPSS für jeden Schritt, also nach jedem Block, ein Regressionsmodell aus. Dadurch kann die Veränderung von Regressionskoeffizienten durch die Aufnahme einer bestimmten weiteren Variablen beobachtet werden und es können Tests durchgeführt werden, ob sich das Modell durch das Hinzufügen des weiteren Blocks verbessert.
Im Rahmen des vorliegenden Beispiels werden alle Variablen im ersten Block eingefügt, um das Beispiel möglichst einfach zu halten.
Hinweise
- Bei Methode wird gewählt, wie die unabhängigen Variablen in das Modell aufgenommen werden.
- Unter Statistiken kann die Kollinearitätsdiagnose angewählt werden (VIF und Toleranz). Der Durbin-Watson-Test gibt Auskunft über die Unabhängigkeit der Fehlerwerte.
- Unter Diagramme kann ein Streudiagramm der standardisierten ZRESID und der vorhergesagten Werte ZPRED erstellt werden. Zudem können das Histogramm der standardisierten Residuen und partielle Regressionsdiagramme angefordert werden.
SPSS-Syntax
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT Besucher
/METHOD=ENTER Preis Werbung CD_Verkauf
/PARTIALPLOT ALL
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/METHOD=ENTER Preis Werbung CD_Verkauf
3.4. Prüfen der Voraussetzungen
Bevor die Resultate der Regressionsanalyse analysiert werden, sollen Voraussetzungen geprüft werden. Dies sind die Linearität des Zusammenhangs, die Gauss-Markov-Annahmen, die Annahmen zur Unabhängigkeit und die Normalverteilung der Fehlerwerte und das Thema der Multikollinearität.
Linearität des Zusammenhangs
Es wurde ein lineares Modell postuliert. Diese Voraussetzung bedeutet im Falle der multiplen Regression, dass der Zusammenhang zwischen der abhängigen Variable und jeder der unabhängigen Variablen linear ist, wenn für die Einflüsse aller übrigen unabhängigen Variablen kontrolliert wird. Dies kann nicht über ein einfaches Streudiagramm der abhängigen und unabhängigen Variablen geprüft werden, wie im Falle der einfachen Regression, da die Beziehung zwischen der abhängigen und einer unabhängigen Variablen von den übrigen unabhängigen Variablen im Modell beeinflusst werden kann. Das einfache Streudiagramm berücksichtigt dies nicht. Dennoch wird es als erster Schritt in der Regel kurz betrachtet. Es kann über das folgende SPSS-Menü erstellt werden:
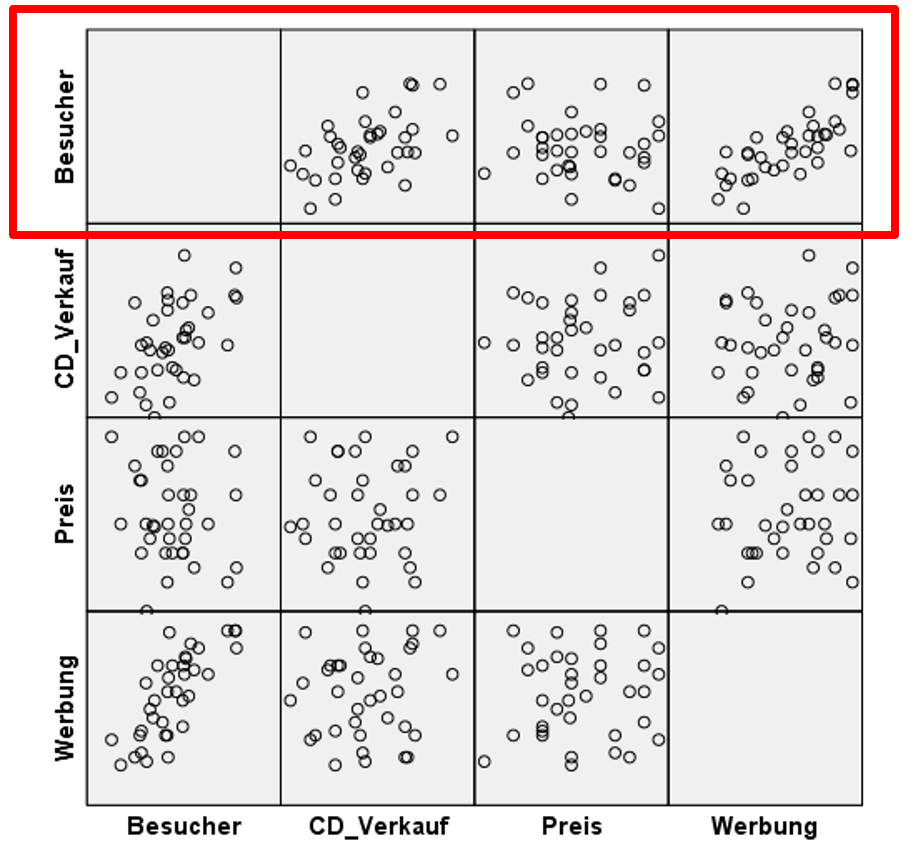
Grafik > Diagrammerstellung > Streu-/Punkt-Diagramm > Streudiagramm-Matrix.
Die Streudiagramm-Matrix gibt einen ersten Überblick über die bivariaten Zusammenhänge zwischen der abhängigen Variable und jeder der unabhängigen Variablen (rote Box in Abbildung 5). Es zeigt sich, dass zumindest bivariat für jede der unabhängigen Variablen eine lineare Beziehung plausibel ist: Die Besucherzahlen scheinen mit steigenden CD-Verkäufen zuzunehmen. Dasselbe gilt für das Werbebudget. Beim Ticketpreis scheint der Zusammenhang weniger deutlich zu sein.
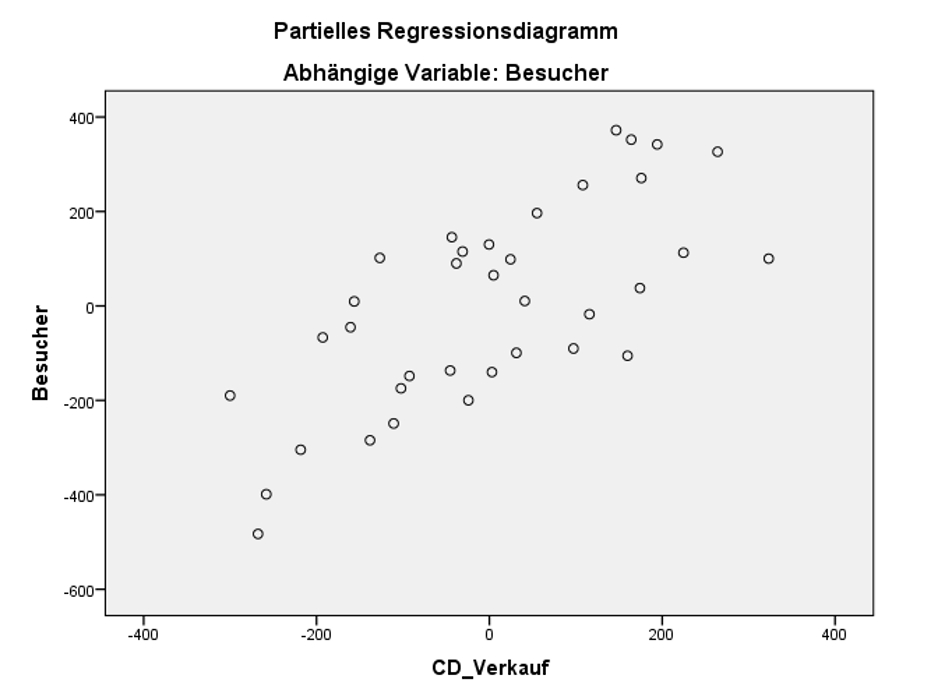
Um genauer zu prüfen, ob Linearität vorliegt, wird empfohlen für jede Variable ein spezielles Streudiagramm, einen sogenannten „Component-plus-residual-Plot“ zu erstellen. In SPSS ist dies nicht direkt implementiert, sondern muss über mehrere Schritte erzeugt werden. Etwas weniger geeignet, aber direkt über den Regressionsdialog erzeugbar sind „Partielle Regressionsdiagramme“. Sie können unter „Diagramme“ angewählt werden („Alle partiellen Diagramme erzeugen“). Abbildung 4 zeigt ein partielles Regressionsdiagramm der Variable CD_Verkauf.
Dieses partielle Regressionsdiagramm für CD_Verkauf zeigt auf der Y-Achse das Residuum, wenn Besucher auf alle unabhängigen Variablen ausser CD_Verkauf regressiert wird. Auf der X-Achse sieht man das Residuum, wenn CD_Verkauf ebenfalls auf alle anderen unabhängigen Variablen regressiert wird. Das heisst, der von allen anderen unabhängigen Variablen nicht erklärte Teil von Besucher wird gegen den von allen anderen unabhängigen Variablen unabhängigen Teil von CD_Verkauf geplottet.
Zeigen die partiellen Regressionsdiagramme aller unabhängigen Variablen eine lineare Beziehung, so wird davon ausgegangen, dass die Voraussetzung der Linearität erfüllt ist. Dies ist in Abbildung 6 für CD_Verkauf der Fall. Auch für die anderen unabhängigen Variablen trifft dies zu. Dies wird hier aber der Übersichtlichkeit halber nicht gezeigt.
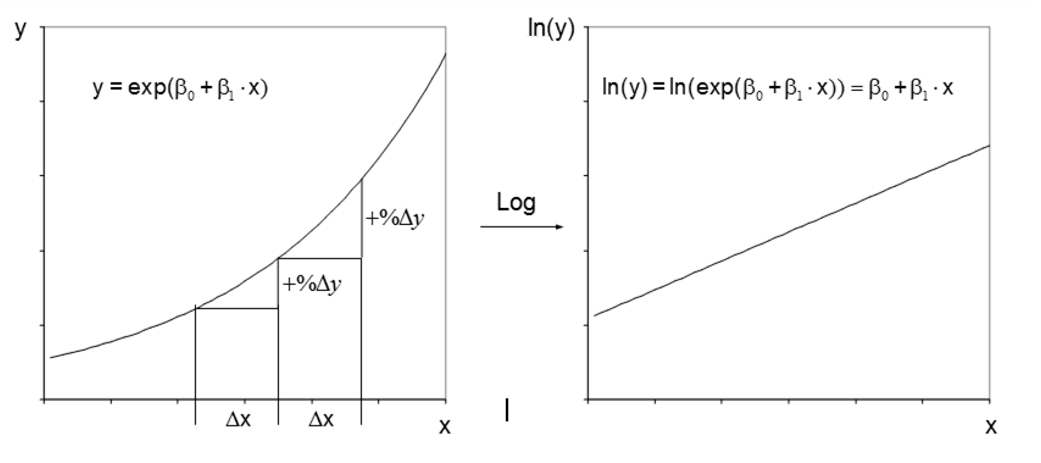
Es gilt anzumerken, dass auch nicht-lineare Zusammenhänge zwischen y und x mittels Regressionsanalyse untersucht werden können. Dazu wird der Zusammenhang vor der Regressionsanalyse derart transformiert, dass er linear wird. Dies geschieht durch eine Transformation von y und/oder x. Anschliessend wird nicht der Zusammenhang zwischen y und x modelliert, sondern zwischen den allenfalls transformierten Variablen.
Ist beispielsweise der prozentuale Anstieg von y konstant, wenn x um eine Einheit erhöht wird, so ist eine Logarithmierung von y angemessen, wie Abbildung 5 verdeutlicht. Während der Zusammenhang zwischen y und x nicht linear ist, ist jener zwischen der transformierten Variable ln(y) und x linear.
Weitere Transformationen sind möglich. Es kann beispielsweise auch x quadriert oder logarithmiert werden oder es könnte die Wurzel von x verwendet werden. Abschliessend soll festgehalten werden: Nicht-lineare Variablen sind möglich und oft sehr nützlich. Davon zu unterscheiden, ist die Voraussetzung der Linearität der Koeffizienten, welche zwingend erfüllt sein muss.
Linearität der Koeffizienten (Gauss-Markov-Annahme 1)
Das postulierte Modell ist linear in den Koeffizienten:
Im vorgestellten SPSS-Dialog können nur Modelle erstellt werden, die linear in den Koeffizienten sind. Nicht-Linearität der Koeffizienten würde bedeuten, dass ein Modell postuliert würde, das beispielsweise (β1)2 oder ln(β1) beinhalten würde.
Zufällige Stichprobe (Gauss-Markov-Annahme 2)
Die Antwort auf die Frage, ob diese Voraussetzung erfüllt ist, wird auf der Basis von Hintergrundwissen zum Datensatz gefunden. Für das Beispiel wird davon ausgegangen, dass die Veranstalter eine zufällige Stichprobe gezogen haben.
Bedingter Erwartungswert (Gauss-Markov-Annahme 3)
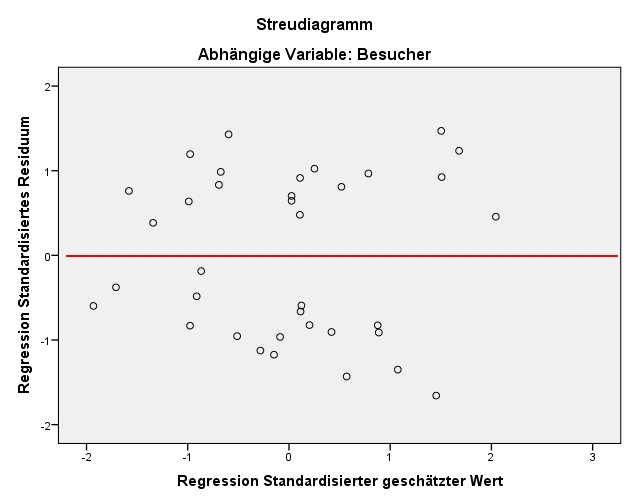
Diese Voraussetzung verlangt, dass der Fehlerwert ε für jeden Wert der unabhängigen Variablen den Erwartungswert 0 hat. Zur Prüfung dieser Annahme wird ein Streudiagramm der standardisierten, geschätzten Werte von y (auf der x-Achse) und der standardisierten Fehlerwerte (Residuen, auf der y-Achse) erzeugt. Es wird anschliessend visuell geprüft, ob über den gesamten Wertebereich der geschätzten Werte der Fehler im Mittel 0 beträgt.
Wie in Abbildung 6 zu erkennen ist, ist es möglich, dass der Mittelwert der Fehlerwerte ungefähr bei 0 liegt: Die negativen und die positiven Abweichungen von 0 auf der y-Achse („gegen oben“ und „gegen unten“) gleichen sich im Mittel etwa aus.
Stichprobenvariation der unabhängigen Variablen (Gauss-Markov-Annahme 4)
Wie die Streudiagramm-Matrix in Abbildung 6 bereits gezeigt hat, weisen alle unabhängigen Variablen Varianz auf.
Homoskedastizität (Gauss-Markov-Annahme 5)
Homoskedastizität bedeutet, dass der Fehler für jeden Wert der unabhängigen Variablen die gleiche Varianz aufweist. Geprüft wird diese Voraussetzung oft im gleichen Streudiagramm, in welchem bereits der bedingte Erwartungswert des Fehlers geprüft wurde. Es wird visuell geprüft, ob über den gesamten Wertebereich der geschätzten Werte der Fehler die gleiche Varianz aufweist. Dies scheint im vorliegenden Beispiel der Fall zu sein (siehe Abbildung 8). Das heisst, es liegt vermutlich Homoskedastizität vor.
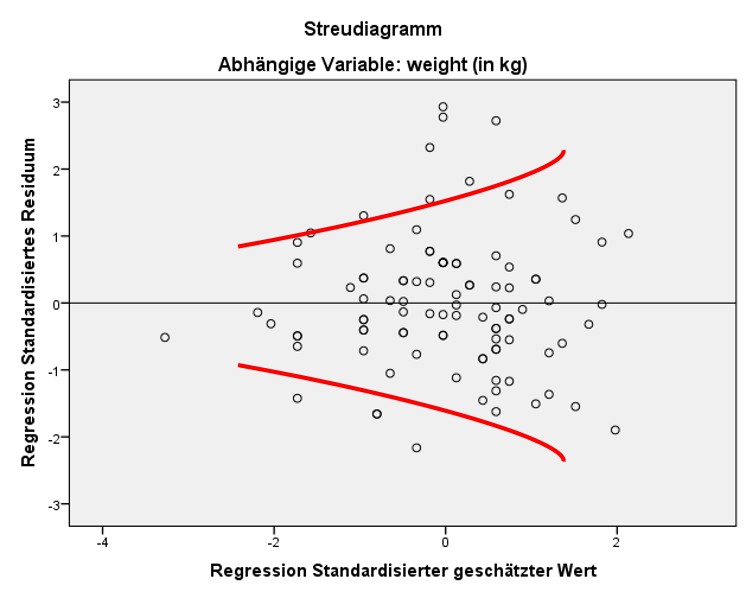
Liegt keine Homoskedastizität vor, der Fehler hat also nicht über den ganzen Wertebereich der geschätzten Werte die gleiche Varianz, so wird von Heteroskedastizität gesprochen. Dies ist daran zu erkennen, dass das Streudiagramm ein eindeutiges Muster aufweist, wie beispielsweise eine Trompetenform (wie in Abbildung 7 dargestellt).
Neben der visuellen Inspektion liegen auch statistische Tests zur Überprüfung dieser Voraussetzung vor, welche in SPSS über Analysieren > Allgemeines lineares Modell > Univariat > Optionen zu finden sind. Dort können beispielsweise der Breusch-Pagan-Test, der Cook-Weisberg-Test oder der White-Test ausgewählt werden (siehe Abbildung 8). Da die Nullhypothese dieser Tests besagt, dass Homoskedastizität besteht, ist ein nicht signifikantes Ergebnis > .05 wünschenswert. Im vorliegenden Beispiel ist der Breusch-Pagan-Test mit .187 nicht signifikant, weshalb von Homoskedastizität ausgegangen werden kann.
Unabhängigkeit des Fehlerwerts
Diese Annahme verlangt, dass die Fehlerterme verschiedener Beobachtungen (hier: Konzerte) nicht zusammenhängen, also keinen Einfluss aufeinander haben (d.h. keine Autokorrelation aufweisen). Auch zur Prüfung dieser Annahme wird auf das Streudiagramm in Abbildung 8 zurückgegriffen. Sind die Fehler voneinander unabhängig, so sollte sich kein Muster zeigen, wie beispielsweise ein wellenförmiger Verlauf. Eine Verletzung dieser Voraussetzung tritt meistens nur dann auf, wenn Zeitreihendaten, geclusterte Beobachtungen (e.g. mehrere Beobachtungen in der gleichen Schulklasse, dem gleichen Haushalt, dem gleichen Wahlbezirk etc.) oder Paneldaten vorliegen (e.g. gleiche Personen mehrfach befragt).
Im vorliegenden Beispiel gibt es keinen Hinweis auf ein Problem, so dass von unkorrelierten Fehlern ausgegangen wird.
Neben der visuellen Inspektion stellt SPSS auch statistische Tests zur Überprüfung dieser Voraussetzung zur Verfügung: den Durbin-Watson-Test. Dessen Teststatistik kann Ausprägungen zwischen 0 und 4 annehmen. Dabei weisen die Werte 0 und 4 auf abhängige Fehlerwerte hin (vollständige Autokorrelation) und ein Wert von 2 auf unabhängige Fehlerwerte (keine Autokorrelation). Wie Abbildung 13 entnommen werden kann, liegt der Wert des Durbin-Watson-Tests bei 1.913, was für unabhängige Fehlerwerte spricht.
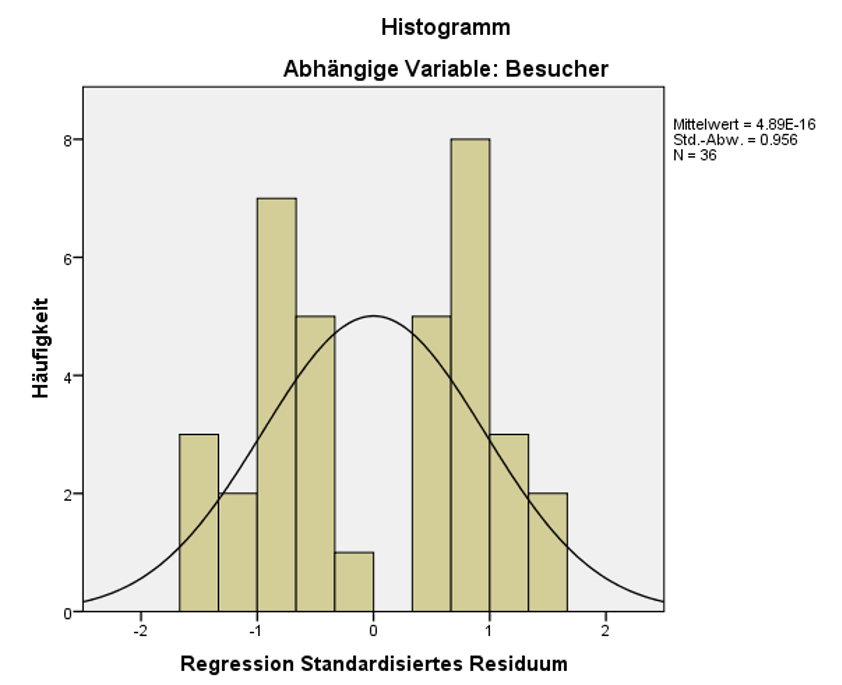
Normalverteilung des Fehlerwerts
Die Residuen sollten näherungsweise normalverteilt sein. Dies wird in der Regel anhand eines Histogramms der standardisierten Residuen visuell beurteilt. Abbildung 8 lässt erkennen, dass die Verteilung des Fehlerwerts bimodal („zweigipflig“) ist. Dies könnte problematisch sein, wird aber in diesem Beispiel vernachlässigt.
Keine Multikollinearität
Diese Voraussetzung verlangt, dass sich die unabhängigen Variablen nicht als lineare Funktion der anderen unabhängigen Variable darstellen lassen dürfen. Ein bestimmtes Mass an Multikollinearität (i.e. die unabhängigen Variablen korrelieren untereinander) lässt sich meist nicht vermeiden. Es sollte allerdings darauf geachtet werden, dass diese nicht zu gross ist, denn Multikollinearität führt zu ungenauen Schätzungen der betroffenen Regressionsparameter. So können in Wirklichkeit bedeutsame unabhängige Variablen nicht signifikante Regressionskoeffizienten aufweisen.
Mittels SPSS können zwei Statistiken berechnet werden, mit denen die unabhängigen Variablen auf Multikollinearität überprüft werden können: der Toleranzwert und der Varianzinflationsfaktor (kurz „VIF“). Es spielt keine Rolle, welche der beiden Statistiken betrachtet wird – die Schlussfolgerung ist die gleich, da die eine lediglich den Kehrwert der anderen darstellt. Beide dienen der Einschätzung der linearen Abhängigkeiten zwischen den unabhängigen Variablen. Der Toleranzwert der Variable xj wird wie folgt berechnet:
Zur Beurteilung wird oft die folgende Faustregel verwendet: Der Toleranzwert soll nicht kleiner als 0.10 und der Varianzinflationsfaktor nicht grösser als 10 sein. Sind die Werte grösser, bzw. kleiner, so liegt keine Multikollinearität vor.
Wie Abbildung 12 entnommen werden kann, liegt für das vorliegende Beispiel keine Multikollinearität vor.
Läge Multikollinearität vor, so müsste dies manuell korrigiert werden: Dazu wird das Regressionsmodell angepasst und erneut berechnet. In der Regel heisst dies, dass eine der betroffenen Variablen ausgeschlossen oder transformiert wird. SPSS berücksichtigt bei der Durchführung der Regressionsanalyse die Multikollinearität nicht, es sei denn, die Multikollinearität ist perfekt (eine Variable kann vollständig durch eine Linearkombination der anderen unabhängigen Variablen beschrieben werden).
Da nun alle Voraussetzungen geprüft worden sind und – zwar nicht ideal jedoch akzeptabel – erfüllt sind, werden das Regressionsmodell als Ganzes und die einzelnen Regressionskoeffizienten auf statistische Signifikanz geprüft.
3.5. Signifikanz des Regressionsmodells
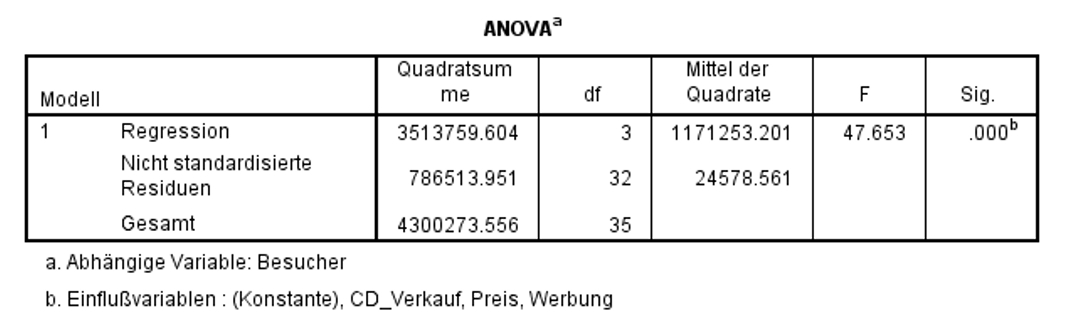
Zur Überprüfung, ob das Regressionsmodell insgesamt signifikant ist, wird ein F-Test durchgeführt. Dieser prüft, ob die Vorhersage der abhängigen Variablen durch das Hinzufügen der unabhängigen Variablen verbessert wird. Das heisst, der F–Test prüft, ob das Modell insgesamt einen Erklärungsbeitrag leistet.
In Abbildung 9 ist zu erkennen, dass das Modell als Ganzes signifikant ist (F(3,32) = 47.653, p < .001). Aus diesem Grund kann die Analyse fortgesetzt werden. Wäre das Modell als Ganzes nicht signifikant, so würde die Analyse nicht fortgesetzt.
3.6. Signifikanz der Regressionskoeffizienten
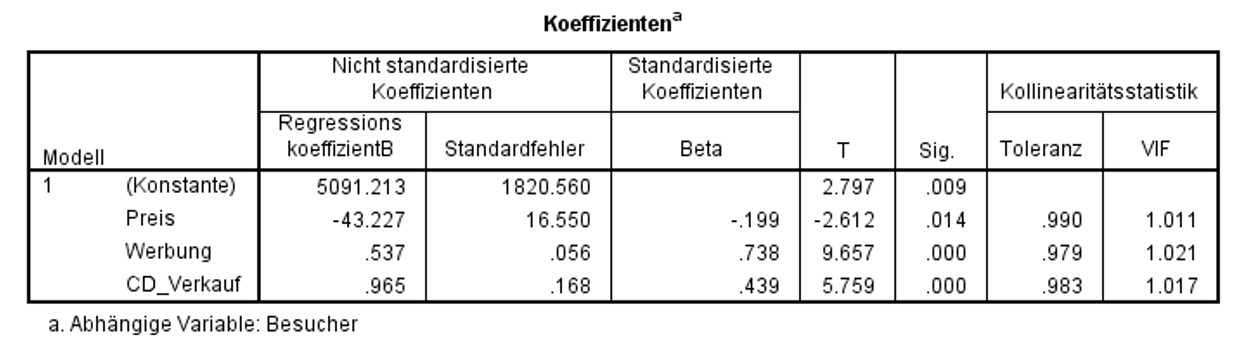
Nun wird geprüft, ob die Regressionskoeffizienten (Betas) ebenfalls signifikant sind. Dabei wird für jeden der Regressionskoeffizienten ein t-Test durchgeführt. Die Ergebnisse des t-Tests können den Spalten „T“ und „Sig.“ in Abbildung 10 entnommen werden.
Abbildung 10 zeigt, dass die t-Tests für den Regressionskoeffizienten von Preis (t = -2.612, p = .014), von Werbung (t = 9.657, p < .001), von CD_Verkauf (t = 5.759, p < .001) und die Konstante (d.h. der Y-Achsenabschnitt; t = 2.797, p = .009) signifikant ausfallen. Eine signifikante Konstante bedeutet, dass der Y-Achsenabschnitt nicht 0 beträgt und damit die Regressionsgerade nicht durch den Ursprung geht. Die signifikanten Koeffizienten der unabhängigen Variablen bedeuten, dass deren Regressionskoeffizienten nicht 0 sind und diese Variablen somit einen signifikanten Einfluss auf Besucher aufweisen.
Somit ergibt sich folgende Regressionsgleichung:
Wie die Gleichung zeigt, weist der Koeffizient der Variable Preis ein negatives Vorzeichen auf. Das bedeutet: Wenn der Preis um eine Einheit (einen Schweizer Franken) steigt, sinkt die Besucherzahl um 43.23 Einheiten (Personen), wenn alle anderen unabhängigen Variablen konstant gehalten werden (sich ihre Werte nicht verändern). Werbung und CD_Verkauf weisen beide einen positiven Koeffizienten auf: Wenn Werbung um eine Einheit (Schweizer Franken) steigt, so steigt die Besucherzahl um 0.54 Einheiten (Personen), alle anderen Variablen konstant gehalten. Nimmt CD_Verkauf um eine Einheit zu (eine CD), so steigen die Besucherzahlen um 0.97 Einheiten (Personen), alle anderen Variablen konstant gehalten.
3.7. Modellgüte
Das sogenannte „R2“ wird auch als „Bestimmtheitsmass“ bezeichnet. Es zeigt, wie gut das geschätzte Modell zu den erhobenen Daten passt. R2 beschreibt, welcher Anteil der Streuung in der abhängigen Variable durch die unabhängigen Variablen erklärt werden kann. R2 kann Werte zwischen 0 und 1 annehmen. 0 bedeutet, dass das Modell keine Erklärungskraft besitzt, 1 bedeutet, dass das Modell die beobachteten Werte perfekt vorhersagen kann. Je höher der R2-Wert, desto besser also die Passung zwischen Modell und Daten (daher engl. „Goodness of fit“).
R2 wird von der Anzahl der unabhängigen Variablen im Modell beeinflusst. Dies ist im Falle der multiplen Regression problematisch, da mehrere unabhängige Variablen in das Modell einbezogen werden. Hier steigt das R2 mit der Anzahl der unabhängigen Variablen, auch wenn die zusätzlichen Variablen keinen Erklärungswert haben. Daher wird R2 nach unten korrigiert („Korrigiertes R2„). Diese Korrektur fällt umso grösser aus, je mehr Variablen im Modell sind, aber umso kleiner, je grösser die Stichprobe ist. Der SPSS-Output enthält immer R2 und das korrigierte R2 (siehe Abbildung 11).
Im vorliegenden Beispiel beträgt das korrigierte R2 .800, was bedeutet, dass 80.0% der Gesamtstreuung in Besucher durch Preis, Werbung und CD_Verkauf erklärt werden kann (Abbildung 13).
3.8. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel wird 80.0% der Gesamtstreuung in der abhängigen Variable durch die unabhängigen Variablen erklärt, doch es stellt sich die Frage, ob dies hoch genug ist, um als bedeutend eingestuft zu werden.
Es gibt verschiedene Arten die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Der Korrelationskoeffizient eignet sich sehr gut, da die Effektstärke dabei immer zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Wenn sich jedoch die Gruppen hinsichtlich ihrer Grösse stark unterscheiden, wird empfohlen, d von Cohen zu wählen, da r durch die Grössenunterschiede verzerrt werden kann.
Das R2, das bei Regressionsanalysen ausgegeben wird, kann in eine Effektstärke f2 nach Cohen (1992) umgerechnet werden. In diesem Fall ist der Wertebereich der Effektstärke zwischen 0 und unendlich.
3.9. Eine typische Aussage
Eine multiple Regressionsanalyse zeigt, dass die Anzahl verkaufter Platten, der Ticketpreis sowie das Werbebudget einen Einfluss auf die Anzahl Konzertbesucher haben, F(3,35) = 47.65, p < .001, n = 36. Steigt der Preis der Konzertkarten um einen Schweizer Franken, so sinkt die Besucherzahl um durchschnittlich 43.23 Personen. Steigt das Werbebudget um einen Franken, nimmt die Anzahl Besucher um 0.54 Personen zu, und verkauft eine Band eine CD mehr, so nimmt die Besucherzahl um durchschnittlich 0.97 Personen zu. 80% der Streuung in der Anzahl Konzertbesuche wird durch die drei unabhängigen Variablen erklärt, was nach Cohen (1992) einem starken Effekt entspricht.