 Quick Start
Quick Start
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen der Faktoranalyse
2.1. Beispiel einer Studie
2.2. Schritt 1: Variablenauswahl
2.3. SPSS-Befehle
2.4. Schritt 2: Eignung prüfen und Extraktion der Faktoren
2.5. Schritt 3: Bestimmen der Anzahl Faktoren
2.6. Schritt 4: Interpretation der Faktoren
2.7. Schritt 5: Summenskalen oder Faktorwerte berechnen
2.8. Eine typische Aussage
Quick Start
| Wozu wird eine Faktorenanalyse verwendet? Die Faktorenanalyse fasst Gruppen von intervallskalierten Variablen zu Faktoren zusammen. SPSS-Menü
Analysieren > Dimensionsreduktion > Faktorenanalyse SPSS-Syntax
FACTOR /VARIABLES Variablen /MISSING LISTWISE /ANALYSIS Variablen /CRITERIA MINEIGEN(1) ITERATE(25) /EXTRACTION PC /CRITERIA ITERATE(25) /ROTATION VARIMAX /SAVE REG(ALL) /METHOD=CORRELATION. SPSS-Beispieldatensatz
Faktoranalyse |
Die Faktorenanalyse fasst Gruppen von intervallskalierten Variablen zu aussagekräftigen und voneinander möglichst unabhängigen Faktoren zusammen.
Sie kann auch eingesetzt werden, um Strukturen in den Daten zu entdecken.
Damit dient die Faktoranalyse in erster Linie der Datenstrukturierung und Datenreduktion. Das Zusammenfassen von Variablen zu Faktoren erleichtert einerseits die Interpretation, andererseits kann in weiterführenden Analysen ein einziger Faktor oder wenige Faktoren anstelle einer grossen Anzahl an Variablen verwendet werden.
Die Faktoranalyse umfasst unterschiedliche Verfahren, welche teilweise verschiedene Zielsetzungen verfolgen. Im Allgemeinen wird zwischen der explorativen und der konfirmatorischen Faktoranalyse unterschieden.
Eine explorative Faktoranalyse (kurz „EFA“) wird verwendet, wenn keine gesicherten Annahmen über die Zusammenhänge zwischen den erhobenen Variablen vorliegen, sondern explorativ nach einer Beziehungsstruktur gesucht wird. Es handelt sich daher um ein strukturentdeckendes Verfahren, das der Hypothesengenerierung dient. Es wird oftmals eingesetzt, wenn ein eigenes Messinstrument entwickelt wird und geprüft werden soll, ob die Items zu einem einzigen oder zu mehreren Faktoren zusammengefasst werden sollen. Beispielsweise bei der Entwicklung einer Skala zur Einstellung zu Fair-Trade-Produkten stellt sich die Frage, ob zwischen einer Einstellung zu Fair-Trade-Lebensmitteln und einer Einstellung zu Fair-Trade-Produkten aus dem Non-Food-Bereich unterschieden werden muss.
Bei einer konfirmatorischen Faktoranalyse (kurz „CFA“, da engl. „Confirmatory Factor Analysis“) hingegen wird geprüft, ob bestimmte erwartete Zusammenhänge zwischen den untersuchten Variablen vorliegen. Daher wird auch von einem hypothesenprüfenden Verfahren gesprochen. Es wird oftmals eingesetzt, wenn ein etabliertes Messinstrument verwendet wird, wie beispielsweise ein Instrument zur Erhebung der „Big Five“. Bei den „Big Five“ handelt es sich um fünf Persönlichkeitsdimensionen, welche je durch eine Reihe von Items abgebildet werden sollen. Es wird erwartet, dass die Items zu jeder Persönlichkeitsdimension einen eigenen Faktor bilden und damit eine Fünf-Faktor-Struktur vorliegt. Mittels der konfirmatorischen Faktoranalyse wird nun geprüft, ob die Daten zur theoretisch erwarteten Struktur passen.
Im vorliegenden Kapitel wird ausschliesslich auf die explorative Faktoranalyse näher eingegangen.
Die Fragestellung der explorativen Faktoranalyse wird oft so verkürzt:
„Lässt sich ein bestimmtes Variablenset durch wenige, voneinander unabhängige Faktoren abbilden?“
1.1. Beispiele für mögliche Fragestellungen
- Lassen sich die Interessen an verschiedenen Berufsrichtungen in übergeordnete Faktoren (wie beispielsweise das Interesse an technischen Berufen, an sozialen Berufen, etc.) zusammenfassen?
- Sollten verschiedene Komponenten der Kundenzufriedenheit unterschieden werden (beispielsweise Zufriedenheit mit der Qualität des Produkts und Zufriedenheit mit der Serviceleistung)?
- Können Verhaltensweisen von Affen in übergeordnete Verhaltensmuster zusammengefasst werden?
1.2. Voraussetzungen der Faktoranalyse
| ✓ | Die Stichprobe ist genügend gross (Faustregel: mindestens 10 Fälle pro Variable) |
| ✓ | Ausreichende Anzahl Variablen (Faustregel: 4 oder mehr pro Faktor) |
| ✓ | Die Variablen sind intervallskaliert (In der Praxis werden jedoch oft auch ordinalskalierte Variablen verwendet.) |
2.1. Beispiel einer Studie
Eine Forschungsgruppe untersuchte Werteinstellungen von Jugendlichen. Zu diesem Zweck liessen sie 1506 Jugendliche einen Fragebogen mit 16 Fragen (Items V01 bis V16) beantworten. Eine Frage ist beispielsweise: „Wie wichtig ist es Ihnen, in einer sicheren Umgebung zu leben?“ Zur Beantwortung wurde eine 6-stufige Likertskala vorgegeben (von 1 „entspricht mir voll und ganz“ bis 6 „entspricht mir überhaupt nicht“). Nun wollen die Forschenden herausfinden, ob die 16 Items zu wenigen übergeordneten Faktoren zusammengefasst werden können.
Der zu analysierende Datensatz enthält neben der Identifikationsnummer der Teilnehmer (ID) die 16 Variablen, V01 bis V16, die in die Faktoranalyse einfliessen.
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Schritt 1: Variablenauswahl
Zunächst muss festgelegt werden, welche Variablen in die Faktoranalyse einfliessen sollen. Dabei sollten nur theoretisch relevante Variablen berücksichtigt werden. Des Weiteren muss eine ausreichende Anzahl Variablen vorhanden sein; als Faustregel gilt vier oder mehr Variablen pro Faktor. Da die Ergebnisse der Faktoranalyse von der Güte der Daten abhängen, sollte diese Auswahl sehr sorgfältig geschehen. Für das Beispiel wurden die 16 Variablen V01 bis V16 ausgewählt, welche im Folgenden auf ihre Eignung geprüft werden. Es ist möglich, dass die weiteren Ergebnisse zeigen würden, dass eine (oder mehrere) der Variablen aus der Analyse entfernt werden sollten.
2.3. SPSS-Befehle
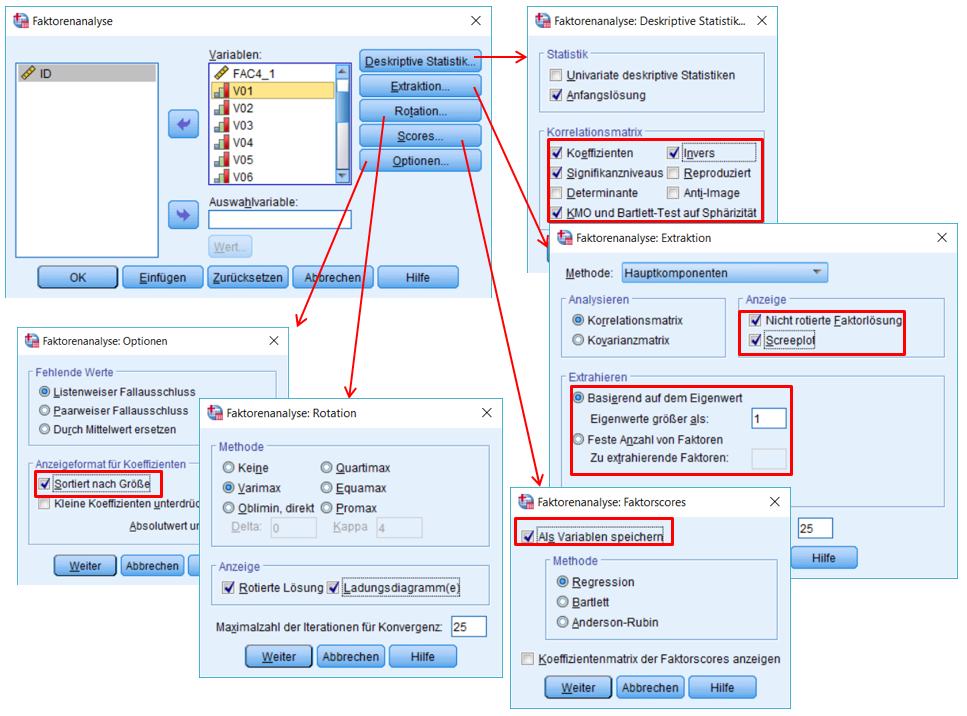
Um das Vorgehen und die grundlegenden Konzepte einer Faktoranalyse zu erläutern und zu veranschaulichen, werden im Folgenden die Schritte in SPSS ausgeführt und erläutert. In der Klicksequenz (Abbildung 2) sind die verwendeten Einstellungen ersichtlich. Die Bedeutung der einzelnen gewählten Optionen wird im weiteren Verlauf dieser Einführung erläutert.
SPSS-Menü: Analysieren > Dimensionsreduktion > Faktorenanalyse
SPSS-Syntax
FACTOR
/VARIABLES V01 V02 V03 V04 V05 V06 V07 V08 V09 V10 V11 V12 V13 V14 V15 V16
/MISSING LISTWISE
/ANALYSIS V01 V02 V03 V04 V05 V06 V07 V08 V09 V10 V11 V12 V13 V14 V15 V16
/PRINT INITIAL CORRELATION SIG KMO INV EXTRACTION ROTATION
/FORMAT SORT
/PLOT EIGEN ROTATION
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/CRITERIA ITERATE(25)
/ROTATION VARIMAX
/SAVE REG(ALL)
/METHOD=CORRELATION.
2.4. Schritt 2: Eignung prüfen und Extraktion der Faktoren
Die Eignung der gewählten Variablen wird in der Regel geprüft, indem die folgenden Aspekte betrachtet werden: bivariate Korrelationen, die inverse Korrelationsmatrix, der KMO-Wert und der Bartlett-Test. Diese werden nun kurz besprochen.
Bivariate Korrelationen
Eine Korrelationsmatrix hilft, einen ersten Eindruck über die Eignung der Variablen für eine Faktoranalyse zu gewinnen. Die Ausgangslage ist für eine Faktoranalyse ideal, wenn voneinander separierte Gruppen hoch korrelierender Variablen vorliegen. Dies würde als Hinweis auf das Vorliegen von Faktoren gedeutet.
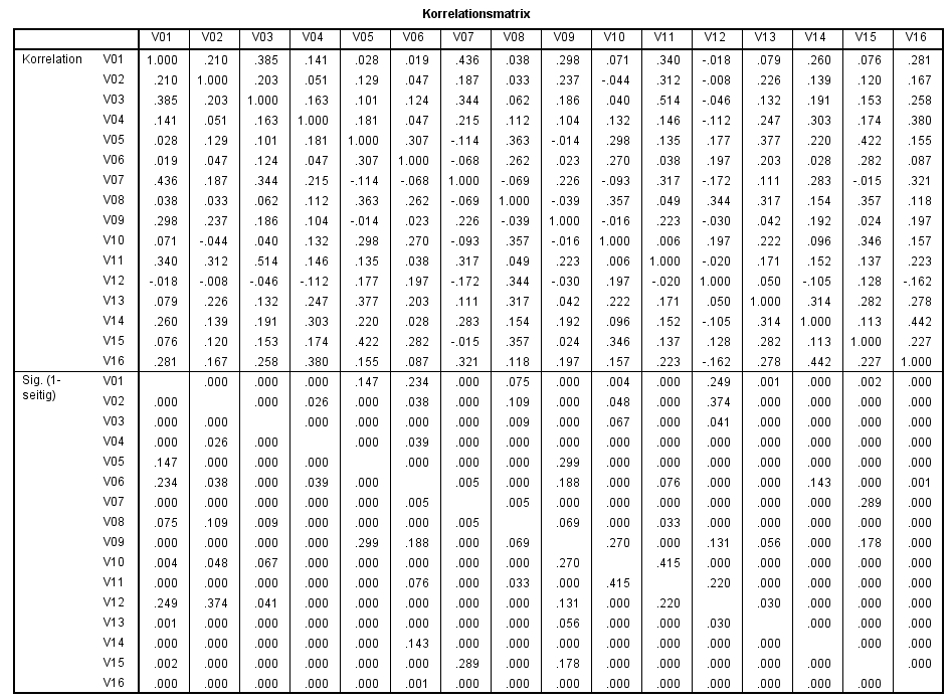
Abbildung 3 zeigt die Korrelationsmatrix, wie SPSS sie im Rahmen einer Faktoranalyse ausgibt. Es handelt sich dabei um eine bivariate Korrelationen nach Pearson. (Alternativ kann auch über das SPSS-Menü Analysieren > Korrelation > Bivariat eine Korrelationsmatrix ausgegeben werden)
Die obere Hälfte der Korrelationsmatrix in Abbildung 3 gibt die Korrelationskoeffizienten wieder, während der unteren Hälfte die Signifikanzniveaus der Korrelationen entnommen werden können. Insgesamt zeigen sich zwischen diversen Variablengruppen hochsignifikante Korrelationen (p < .001).
Da die Signifikanz nicht nur von der Stärke des Zusammenhangs, sondern auch von der Stichprobengrösse beeinflusst wird, bedeutet „signifikant“ jedoch nicht zwingend „bedeutsam“. Es gibt verschiedene Arten, die Stärke einer Korrelation zu beurteilen. Der Korrelationskoeffizient r eignet sich sehr gut als Mass für die Effektstärke, da er stets zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Die Höhe kann anhand der Einteilung der Effektstärke nach Cohen (1992) beurteilt werden:
r = .10 entspricht einem schwachen Effekt
r = .30 entspricht einem mittleren Effekt
r = .50 entspricht einem starken Effekt
Damit entspricht eine Effektstärke von r = .344 (Korrelation zwischen V08 und V12) beispielsweise einem mittleren Effekt.
Auf der Basis der Korrelationsmatrix alleine kann jedoch nicht entschieden werden, ob die Zusammenhänge zwischen den Variablen durch dahinterliegende Faktoren erklärt werden können. Sie dient lediglich als erster Anhaltspunkt.
Inverse der Korrelationsmatrix
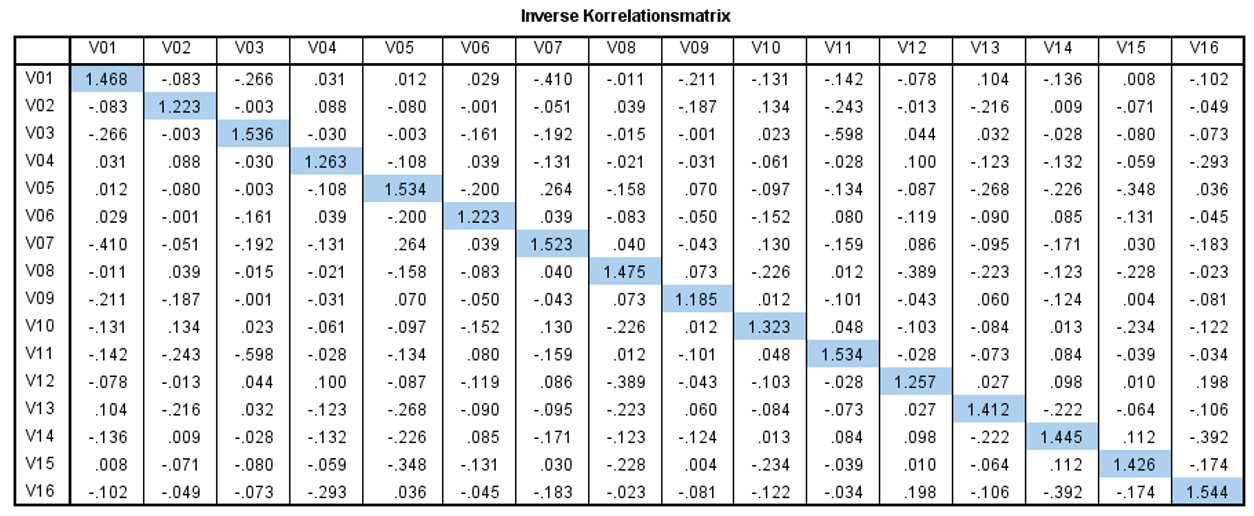
Eine Korrelationsstruktur eignet sich für eine Faktoranalyse, wenn die inverse Korrelationsmatrix eine Diagonalmatrix darstellt. Eine Matrix ist dann diagonal, wenn die Werte ausserhalb der Diagonalen nahe 0 sind, während die Werte auf der Diagonalen deutlich höher liegen. Dabei handelt es sich jedoch lediglich um ein optisches Hilfsmittel zur Beurteilung der Eignung.
Wie Abbildung 4 entnommen werden kann, sind im Beispiel die Werte ausserhalb der Diagonalen deutlich näher bei 0 als jene auf der Diagonalen. Dies ist ein weiterer Hinweis dafür, dass sich die Variablen für eine Faktoranalyse eignen.
KMO-Wert und Bartlett-Test
Kaiser, Meyer und Olkin (KMO) haben ein Standardprüfverfahren für die Eignung der Daten für eine Faktoranalyse entwickelt („Measure of Sampling Adequacy“ (MSA)). Die MSA-Werte beziehen sich jedoch auf einzelne Variablen. Der von SPSS ausgegebene KMO-Wert stellt eine Verallgemeinerung der MSA-Werte für alle Variablen gemeinsam dar. Der KMO-Wert ist ein Mass dafür, ob die partiellen Korrelationen zwischen den Variablen klein sind. Je kleiner diese sind, desto höher ist der KMO.
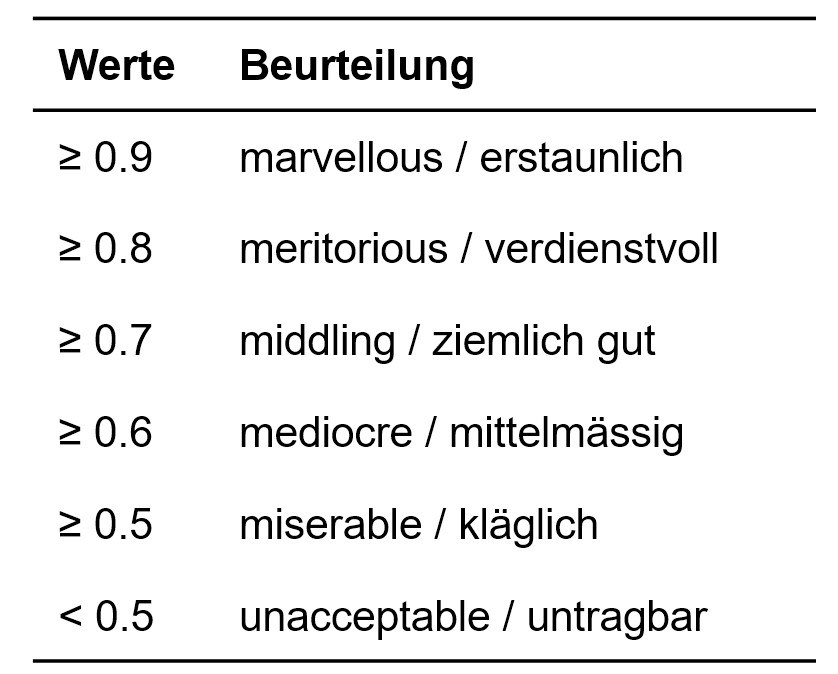
Der KMO nimmt Werte zwischen 0 und 1 an. Es gilt die Faustregel, dass der KMO-Wert mindestens .60 betragen sollte, um mit der Faktoranalyse fortzufahren. Kaiser (1990) schlägt als untere akzeptable Grenze .50 vor, wünschenswert sei jedoch ein Wert über .80. Zur differenzierteren Beurteilung dieser Prüfgrösse wurden die Werte in Abbildung 5 vorgeschlagen.
Wie Abbildung 6 zeigt, beträgt der KMO-Wert des vorliegenden Beispiels .808 („Mass der Stichprobeneigung nach Kaiser-Meyer-Olkin) und ist damit als „verdienstvoll“ einzustufen (vgl. Abbildung 5). Somit gibt es keinen Anlass, die Analyse zu unterbrechen.
Zusätzlich kann anhand des Bartlett-Tests die Nullhypothese geprüft werden, ob die Variablen vollständig unkorreliert sind. Dieser Test setzt jedoch normalverteilte Daten voraus.
Für das Beispiel bestätigt der Bartlett-Test, dass die Variablen nicht vollständig unkorreliert sind (Chi-Quadrat(120) = 4672.19, p < .001). Daher wird mit der Analyse fortgefahren.
Extraktionsmethode
Es gibt verschiedene Methoden zur Extraktion von Faktoren. Am häufigsten werden die sogenannte „Hauptkomponentenanalyse“ und die „Hauptachsenanalyse“ eingesetzt. Beide Methoden lassen keine direkten Rückschlüsse über die Population zu (lediglich über die Stichprobe). Die Übertragbarkeit einer gefundenen Struktur auf die Population zeigt sich erst durch erneute Analysen an weiteren Stichproben.
In mathematischer Hinsicht sind sich die beiden Verfahren sehr ähnlich und führen auch in den meisten Fällen zu ähnlichen Ergebnissen. Sie unterscheiden sich jedoch deutlich bezüglich der Bedeutung der Kommunalitäten und der Interpretation der Faktoren.
Die Hauptkomponentenanalyse (kurz „PCA“, da engl. „Principal Component Analysis“) ist das Standardverfahren in SPSS. Das Ziel ist es, einen möglichst hohen Anteil der Gesamtvarianz in den Variablen zu erklären. Die so entdeckten Faktoren werden als übergeordnete Begriffe aufgefasst, die die zum Faktor gehörigen Variablen zusammenfassen. Die Faktoren werden auch als „Komponenten“ bezeichnet. Streng genommen wird die Hauptkomponentenanalyse nicht zur Faktoranalyse gezählt, wenngleich viele Lehrbücher sie – wie im vorliegenden Fall auch – im Rahmen der Faktoranalyse besprechen und viele Statistikprogramme (wie SPSS) sie als Option einer Faktoranalyse im engeren Sinn implementiert haben.
Bei Hauptachsenanalyse (kurz „PAF“, da engl. „Principal Axis Factoring“) besteht das Ziel darin, die gemeinsame Varianz der Variablen zu erklären. Die so entdeckten Faktoren werden als latente Variablen verstanden. Sie stellen in diesem Verständnis die Ursache für die Ausprägungen der Variablen dar. Sie werden also kausal interpretiert.
Im vorliegenden Beispiel wird ausschliesslich auf die Hauptkomponentenanalyse eingegangen, da diese am häufigsten zum Einsatz kommt.
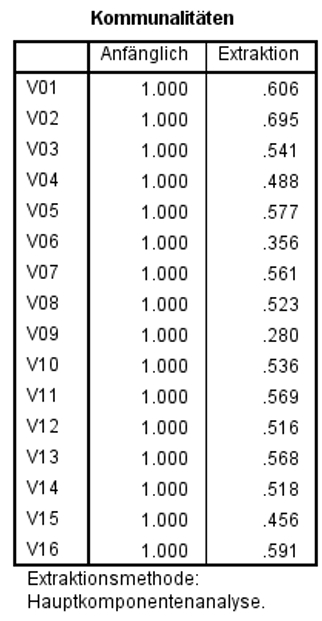
Kommunalitäten
Die Kommunalitäten („Gemeinsamkeiten“) beschreiben den Anteil an der Gesamtvarianz einer Variablen, der durch alle Faktoren gemeinsam erklärt werden kann. Die Kommunalität gibt folglich an, in welchem Ausmass eine Variable durch die Faktoren erklärt wird. Wie die Kommunalitäten bestimmt werden, hängt von der gewählten Extraktionsmethode ab.
Wie Abbildung 7 entnommen werden kann, liegen die meisten Kommunalitäten des vorliegenden Beispiels um .50 herum. Das bedeutet, dass ungefähr die Hälfte der Varianz dieser Variablen durch die extrahierten Faktoren erklärt werden kann. Die Kommunalität des Items V09 ist mit .280 eher niedrig („nur“ 28% erklärte Varianz).
2.5. Schritt 3: Bestimmen der Anzahl Faktoren
Zur Bestimmung der Anzahl Faktoren gibt es kein eindeutiges mathematisches Verfahren. Bei dieser Entscheidung spielen theoretische Überlegungen eine zentrale Rolle, aber die folgenden Kriterien geben weitere Anhaltspunkte: das Kaiser-Kriterium, der Screeplot, sowie die Interpretierbarkeit der Lösung.
Theoretische Überlegungen inhaltlicher Art
Für das vorliegende Beispiel werden aufgrund früherer Studien zum Thema „Werteinstellungen“ drei Faktoren erwartet.
Das Kaiser-Kriterium („Eigenwert-Regel“)
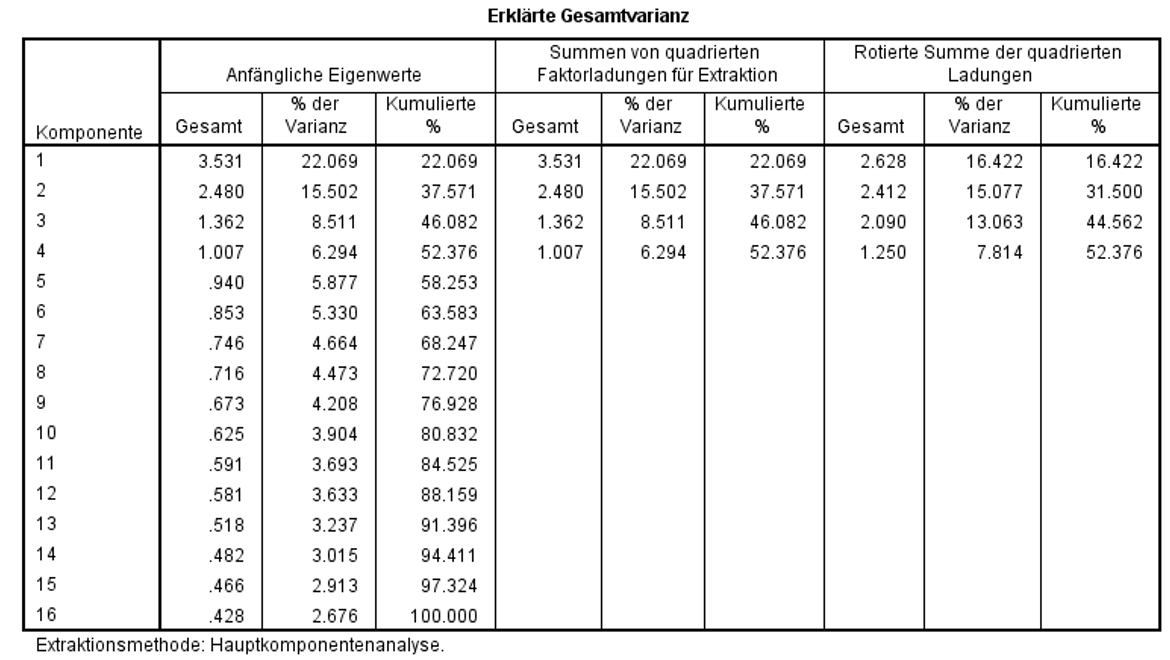
Der Eigenwert eines Faktors gibt an, wie viel der Gesamtvarianz aller Variablen durch diesen Faktor erklärt wird. SPSS normiert zu erklärende Gesamtvarianz auf die Anzahl der Variablen, im vorliegenden Fall also auf 16. Welcher Faktor welchen Anteil dieser normierten Gesamtvarianz erklären kann, kann der linken Spalte „Gesamt“ in Abbildung 8 entnommen werden.
Das sogenannte „Kaiser-Kriterium“ (auch „Eigenwert-Regel“) besagt, dass nur Faktoren extrahiert werden sollen, deren Eigenwert grösser als 1.0 ist.
SPSS wählt die Anzahl Faktoren strikt anhand dieses Kriteriums, sofern der Anwender / die Anwenderin keine feste Anzahl Faktoren vorgibt. Das Kaiser-Kriterium ist zwar sehr verbreitet, doch die Festlegung des Grenzwerts auf 1.0 ist nicht unumstritten.
Wie Abbildung 8 entnommen werden kann, gibt es vier Faktoren mit Eigenwerten grösser als 1.0, wobei der vierte Faktor mit einem Eigenwert von 1.007 lediglich äusserst knapp über dem kritischen Wert liegt.
Die mittlere Spalte „Kumulierte %“ zeigt, dass diese 4 Faktoren zusammen 52.4% der Varianz aller Variablen erklären.
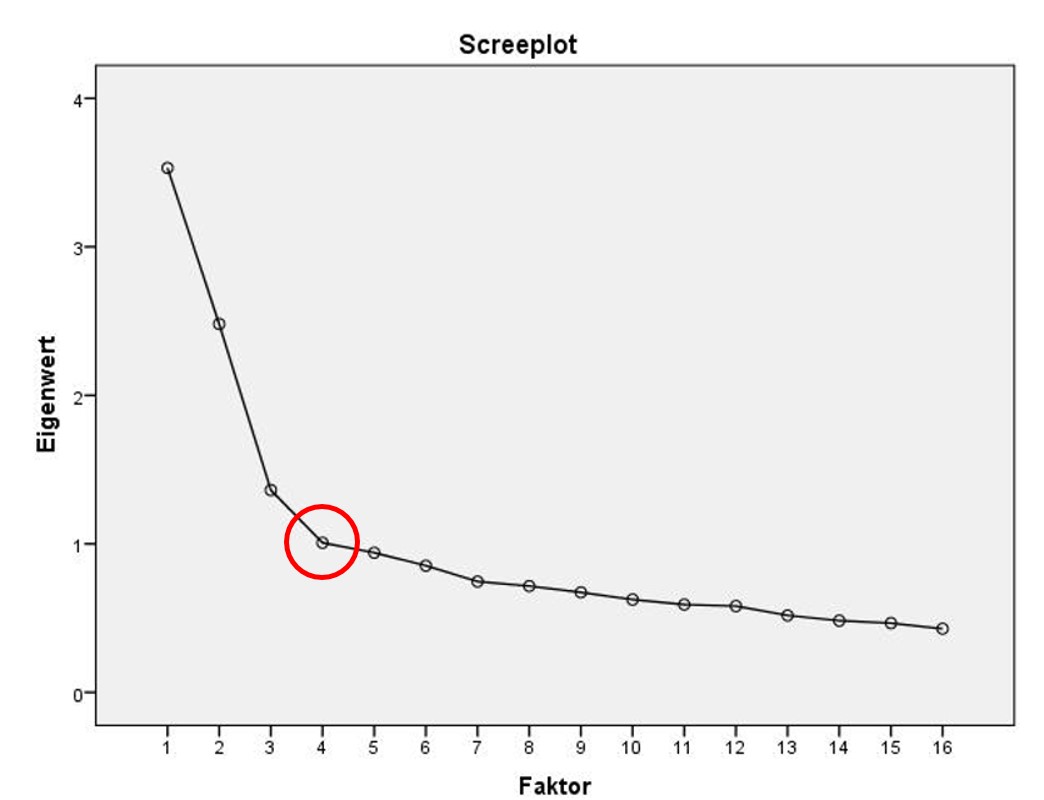
Im Screeplot in Abbildung 9 liegt der Ellbogen bei 4 Faktoren. Dies deutet auf eine Drei-Faktoren-Lösung hin, denn der Ellbogen selbst wird nicht gezählt.
Interpretierbarkeit der Lösung
Als weitere Hilfe kann die inhaltliche Interpretierbarkeit der unterschiedlichen Lösungen verglichen werden. Dazu würden die rotierten Komponentenmatrizen der Lösung mit drei und mit vier Faktoren betrachtet. Dies wird an dieser Stelle übersprungen. Diese Betrachtung würde für das Beispiel jedoch zeigen, dass die Vier-Faktoren-Lösung schwierig zu interpretieren ist (Querladungen), während die Lösung mit drei Faktoren hinreichend klar ist. Auf die Lösung mit drei Faktoren wird entsprechend weiter unten näher eingegangen.
Abwägen zwischen den verschiedenen Kriterien
Die besprochenen Kriterien ergeben für das vorliegende Beispiel widersprüchliche Befunde. Theoretische Überlegungen lassen drei Faktoren erwarten. Der Screeplot weist ebenfalls auf drei Faktoren hin, wohingegen die Eigenwert-Regel vier Faktoren nahelegt. Werden die Eigenwerte genauer betrachtet, so zeigt sich, dass der vierte Faktor einen Eigenwert von 1.007 aufweist und somit nur knapp über dem Grenzwert zur Aufnahme liegt (1.0). Die empirischen Ergebnisse zur Lösung mit vier Faktoren sind schlecht interpretierbar, während die Drei-Faktor-Lösung auf den ersten Blick inhaltlich plausibel erscheint.
Dies spricht insgesamt dafür, die Drei-Faktor-Lösung genauer zu betrachten. Ist die Zuordnung der Variablen auf die drei Faktoren inhaltlich sinnvoll und hinreichend eindeutig, so kann von drei Faktoren ausgegangen werden.
Festlegen der Anzahl Faktoren in SPSS
SPSS legt die Anzahl Faktoren gemäss dem Kaiser-Kriterium fest und gibt die weiteren Teile der Ausgabe entsprechend aus. Entscheidet man sich für eine andere Anzahl Faktoren, so muss die Faktoranalyse mit modifizierten Einstellungen wiederholt werden: In der Eingabemaske muss bei „Extraktion“ unter „Feste Anzahl Faktoren“ die gewünschte Zahl eingegeben werden (siehe Klicksequenz in Abbildung 2). Der SPSS-Output bleibt dabei nahezu identisch, einzig die Tabellen „Erklärte Gesamtvarianz“, „Komponentenmatrix“ und „Rotierte Komponentenmatrix“ ändern sich dahingehend, dass nun die gewünschte Anzahl Faktoren aufgeführt ist. Lediglich die „Rotierte Komponentenmatrix“ muss zur Interpretation neu betrachtet werden.
(SPSS kann die Variablen nach Ladungshöhe sortiert ausgeben. Dies kann die Interpretation erleichtern. Dazu muss unter „Optionen“ „Sortiert nach Grösse“ angewählt werden.)
2.6. Schritt 4: Interpretation der Faktoren
Rotation der Lösung
Zur einfacheren Interpretation der Faktoren empfiehlt es sich, eine sogenannte „Rotation“ vorzunehmen. Es wird zwischen orthogonalen (rechtwinkligen) und obliquen (schiefwinkligen) Rotationen unterschieden.
Die am häufigsten eingesetzte orthogonale Rotation ist die Varimax-Rotation. Dabei wird die Unabhängigkeit der entdeckten Faktoren gewahrt, das heisst, sie bleiben unkorreliert. Schiefwinklige Rotationen dagegen, wie beispielsweise „Oblimin, direkt“, lassen Korrelationen zwischen den Faktoren zu. Obschon in der Praxis „Varimax“ sehr häufig anzutreffen ist, kann oblique Rotation eingesetzt werden, wenn es starke theoretische Gründe gibt, dass die Faktoren korrelieren, oder sofern eine oblique Rotation empirisch eine nicht zu vernachlässigende Korrelation aufzeigt.
Faktorladungen
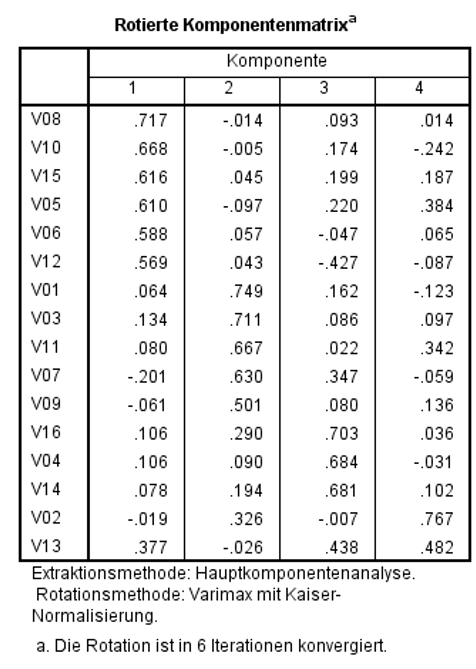
Abbildung 10 zeigt die rotierten Faktorladungen der Beispieldaten. Eine Faktorladung einer Variablen ist die Korrelation zwischen der Variable und dem Faktor. Beispielsweise korrelieren also die Variable V08 und Faktor 1 mit .710. Eine typische Aussage ist „Die Variable V08 lädt mit .710 auf Faktor 1.“
Theoretisch sind Werte zwischen -1 und +1 möglich. Der Betrag der Faktorladung zeigt an, wie eng eine Variable mit einem Faktor zusammenhängt: Beträge nahe bei 0 zeigen an, dass kaum ein Zusammenhang besteht. Je höher der Betrag, desto enger ist der Zusammenhang.
Zuordnung der Variablen auf die Faktoren
Um die Faktorladungen und die Zuordnung der Variablen auf die Faktoren zu beurteilen, wird die rotierte Komponentenmatrix betrachtet (Abbildung 10). Grundsätzlich wird jede Variable dem Faktor zugeordnet, auf den sie am höchsten lädt. Doch wie hoch muss eine Faktorladung sein, bevor sie interpretiert werden sollte?
Es gibt unterschiedliche mögliche Faustregeln:
- Faktorladungen unter ± .20 sollten nicht berücksichtigt werden. Weist ein Item auf keinen Faktor eine höhere Ladung auf, so wird empfohlen, das Item zu entfernen und die Analyse erneut durchführen.
- Faktorladungen von ± .30 bis ± .40 sind minimal akzeptabel, höhere Werte sind jedoch wünschenswert (insbesondere bei kleinen Stichproben und bei einer kleinen Anzahl Variablen).
- Unabhängig von der Stichprobengrösse: Ein Faktor kann interpretiert werden, wenn mindestens 4 Variablen eine Ladung von ± .60 oder mehr aufweisen oder wenn mindestens 10 Variablen eine Ladung von ± .40 oder mehr aufweisen.
- Bei n < 300 sollten Faktoren mit ausschliesslich geringen Ladungen nicht interpretiert werden.
Für das Beispiel wurden in der rotierten Komponentenmatrix alle Faktorladungen ab ± .30 manuell eingefärbt. Es zeigt sich, dass alle Variablen stärkere Faktorladungen als ± .20 aufweisen und dass die meisten Variablen ausschliesslich auf eine Variable höher als ± .30 laden. Damit sind die meisten Variablen klar einem Faktor zuordbar.
Querladungen
Eine Querladung liegt vor, wenn eine Variable hoch auf mehr als einen Faktor lädt. Davon wird gesprochen, wenn eine Variable zwei oder mehr Faktorladungen aufweist, die stärker als ± .30 oder ± .40 sind. Dies bedeutet, dass das Item (inhaltlich) mit mehreren Faktoren zusammenhängt. Es korreliert mit anderen Items, die auf die betroffenen Faktoren laden.
Ist das Ziel, scharf abgegrenzte Faktoren zu finden und daraus beispielsweise Summenskalen zu bilden, so wird zur Beurteilung der Querladung die Differenz zwischen den Ladungen betrachtet.
- Ist die Differenz gross (± .20), so kann die Variable jenem Faktor zugeordnet werden, auf den sie am höchsten lädt.
- Ist die Differenz gering (± .20), so kann die Variable keinem Faktor zugeordnet werden. Oft wird eine solche Variable ausgeschlossen und die Analyse wird erneut durchgeführt (es sei denn, theoretische Gründe sprechen deutlich dagegen).
Ist das Ziel, Gemeinsamkeiten von Konzepten aufzuzeigen, so sind Querladungen von theoretischem Interesse und werden beibehalten. Sie müssen jedoch theoretisch plausibel sein.
Im Beispiel sind die Namen der Variablen mit Querladungen in der rotierten Komponentenmatrix fett gedruckt.
- Für die Variable V07 ist die Differenz der Ladungen hinreichend gross, so dass die geringere der beiden Ladungen vernachlässigt wird und die Variable wird Faktor 2 zugeordnet.
- Für die Variablen V12 und V13 sind die beiden Ladungen jeweils ähnlich stark, so dass diese Variablen empirisch jeweils beiden Faktoren, auf die sie laden, zugeordnet werden könnten. Diese Querladungen dürfen bei der Interpretation nicht vernachlässigt werden.
Inhaltliche Interpretation der Faktoren
Die Interpretation der Faktoren ist ein subjektiver Prozess der Sinnzuschreibung. Wichtig ist, dass die Interpretation stets aufgrund sachlicher und durch die Fachliteratur gut begründbarer Überlegungen erfolgen muss.
Um die Interpretation zu erleichtern, wird oftmals eine Tabelle erstellt, in der die Variablen innerhalb der jeweiligen Faktoren nach absteigendem Ladungsbetrag aufgeführt werden. Dabei sollte das Vorzeichen der Ladung oder der Wert der Ladung notiert werden. Zudem wird auch der Wortlaut der Items betrachtet, insbesondere des am höchsten auf den jeweiligen Faktor ladenden Items.
Aufbauend auf Abbildung 11 ist für das vorliegende Beispiel die folgende inhaltliche Interpretation der Faktoren denkbar:
- Faktor 1 – Wunsch nach Sicherheit und Stabilität: Die Variablen zu Faktor 1 beinhalten Themen wie Sicherheit und normkonformes Verhalten. Die aktuelle Situation soll beibehalten und Wandel vermieden werden.
- Faktor 2 – Wunsch nach Abenteuer und Genuss: Die Variablen befassen sich mit dem Wunsch nach Neuem, Spannung und Genuss. Es handelt sich dabei um lustbetontes und risikosuchendes Verhalten.
- Faktor 3 – Wunsch nach sozialem Status: Die Variablen dieses Faktors beschreiben den Wunsch nach Anerkennung, Bewunderung, Reichtum und Respekt
Umgang mit den nicht-vernachlässigbaren Querladungen
- V12 lädt auf Faktor 1 (.508) und auf Faktor 3 (-.464). Dies ist inhaltlich plausibel. Es macht Sinn, dass Bescheidenheit positiv mit dem Wunsch nach Sicherheit und Stabilität und gleichzeitig negativ mit dem Wunsch nach sozialem Status korreliert.
- Die beiden Ladungen von V13 auf die Faktoren 1 (.493) und 3 (.418) sind inhaltlich ebenfalls plausibel. Einerseits kann der Wunsch nach Respekt dem Bedürfnis nach sozialem Status (Faktor 3) und anderseits dem Bedürfnis nach Sicherheit und Stabilität (Faktor 1) zugeschrieben werden.
Da die Querladungen inhaltlich plausibel sind, wird die Entscheidung, welchen Faktoren diese beiden Items zugeschrieben werden, aufgrund theoretischen Vorwissens getroffen: V12 wird Faktor 1 und V13 Faktor 3 zugeschrieben.
2.7. Schritt 5: Summenskalen oder Faktorwerte berechnen
In einem fünften Schritt können Faktorwerte oder Summenskalen berechnet werden. Diese können in weiteren Analysen anstelle der ursprünglichen Variablen verwendet werden.
Faktorwerte berechnen
SPSS speichert im Zuge einer Faktoranalyse Faktorwerte als neue Variablen im Datensatz (z.B. FAC1_1, FAC1_2), sofern dies unter „Werte“ angewählt wurde. Meist wird dazu die „Regressionsmethode“ gewählt. SPSS gibt zudem eine Komponententransformationsmatrix aus, wie Abbildung 12 zeigt.
Diese Matrix gibt die Beziehung zwischen den Faktorwerten wieder. Sind Faktorwerte unkorreliert, so betragen die Werte der Diagonalen 1 und alle anderen 0. Für den vorliegenden Datensatz gibt es jedoch Korrelationen unter den Faktoren (Komponenten).
Summenskalen berechnen
Alternativ kann auch für jeden Faktor eine Summenskala berechnet werden. Dies geschieht via SPSS-Menü Transformieren > Variablen berechnen… Dabei werden die jeweiligen Items eines Faktors addiert (und, falls erwünscht, durch die Anzahl Variablen im Faktor dividiert, so dass ein Mittelwert entsteht). Das Ergebnis wird als neue Variable gespeichert. Es empfiehlt sich, für die Items, die addiert werden sollen, vorab eine Reliabilitätsanalyse durchzuführen (Analysieren > Skala > Reliabilitätsanalyse…).
2.8. Eine typische Aussage
Die Struktur des Instruments zur Erhebung der Werteinstellungen (V01 bis V16) wurde mittels einer explorativen Faktoranalyse geprüft. Sowohl der Bartlett-Test (Chi-Quadrat(120) = 4672.19, p < .001) als auch das Kaiser-Meyer-Olkin Measure of Sampling Adequacy (KMO = .808) weisen darauf hin, dass sich die Variablen für eine Faktoranalyse eignen. So wurde eine Hauptkomponentenanalyse mit Varimax-Rotation durchgeführt. Obwohl diese auf das Vorliegen von vier Faktoren mit Eigenwerten grösser als 1.0 hinweist, wurde aufgrund des Screeplots und theoretischer Überlegungen eine Drei-Faktor-Lösung gewählt, welche 46.1% der Varianz erklärt. Damit liegen drei Faktoren vor: „Wunsch nach Sicherheit und Stabilität“, „Wunsch nach Abenteuer und Genuss“ sowie „Wunsch nach sozialem Status“. Die gefundenen Querladungen deuten an, dass der dritte Faktor nicht ganz klar von den beiden anderen zu trennen ist. Aufgrund inhaltlichen Vorwissens kann diese Lösung trotzdem angenommen werden.