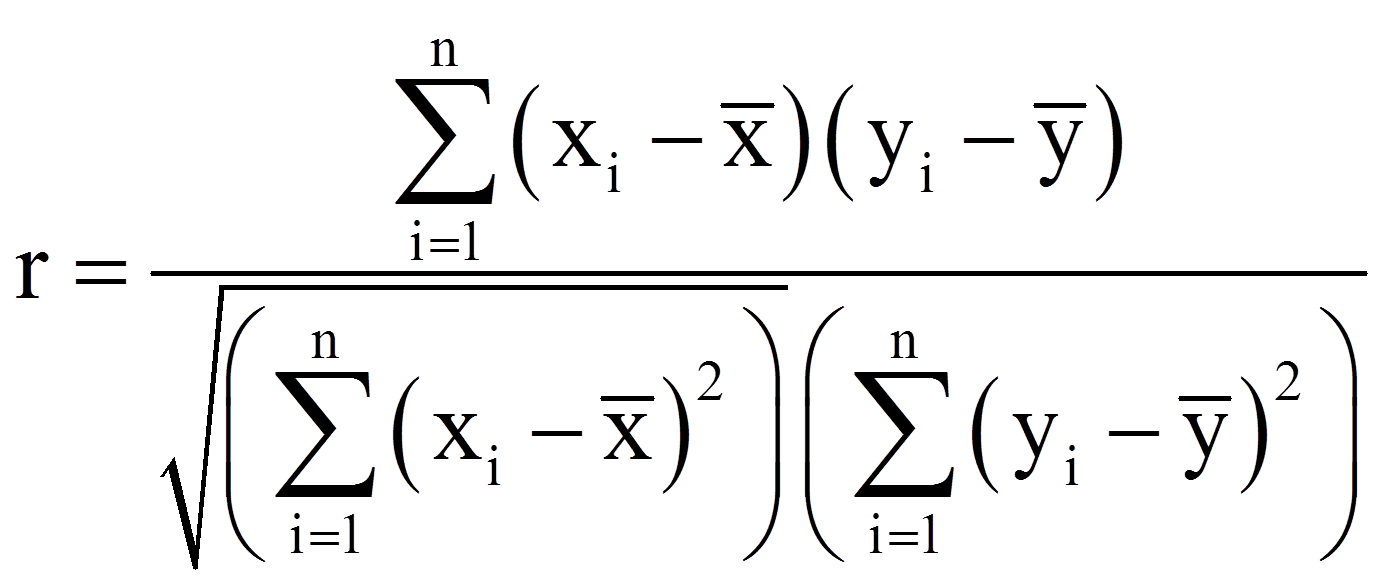 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Grafische Veranschaulichung des Zusammenhangs
2.3. Berechnung des Korrelationskoeffizienten
3. Korrelation mit SPSS
3.1. SPSS-Befehle
3.2. Deskriptive Statistik
3.3. Ergebnisse der Korrelationsanalyse
3.4. Berechnung des Bestimmtheitsmasses
3.5. Berechnung der Effektstärke
3.6. Eine typische Aussage
Quick Start
| Wozu wird eine Korrelation nach Bravais-Pearson verwendet? Die Korrelation nach Bravais-Pearson berechnet den linearen Zusammenhang zweier intervallskalierter Variablen. SPSS-Menü
Analysieren > Korrelation > Bivariat SPSS-Syntax
CORRELATIONS /VARIABLES= Variablen /PRINT=TWOTAIL NOSIG /STATISTICS DESCRIPTIVES SPSS-Beispieldatensatz
Korrelation |
1. Einführung
Die Korrelation nach Bravais-Pearson berechnet den linearen Zusammenhang zweier intervallskalierter Variablen.
Da stets der Zusammenhang zwischen zwei Variablen untersucht wird, wird von einem „bivariaten Zusammenhang“ gesprochen.
Zwei Variablen hängen dann linear zusammen, wenn sie linear miteinander variieren (also kovariieren). Sie können dies in unterschiedlicher Weise tun:
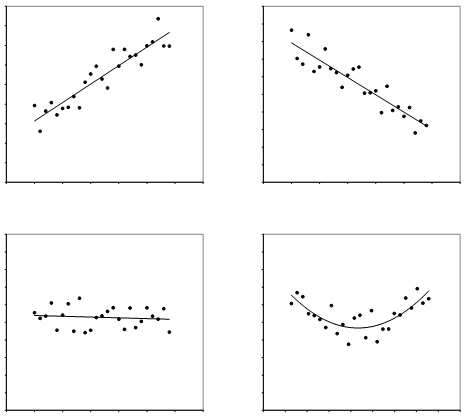
- Gleichsinnige oder positive Korrelation: Hohe (tiefe) Ausprägungen der einen Variablen gehen mit hohen (tiefen) Ausprägungen der zweiten Variablen einher (Abbildung 1: oben links). Zum Beispiel: Je mehr eine Person isst, desto ausgeprägter ist ihr Sättigungsgefühl. Je weniger jemand isst, desto geringer ist das Sättigungsgefühl.
- Gegenläufige oder negative Korrelation: Hohe Werte der einen Variablen gehen mit tiefen Werten der anderen einher (Abbildung 1: oben rechts). Zum Beispiel: Je mehr jemand schläft, desto weniger müde ist er. Je weniger jemand schläft, desto müder ist er.
Auch nicht-lineare Zusammenhänge sind möglich, wie beispielsweise eine u-förmige (Abbildung 1: unten rechts) oder umgekehrt u-förmige Kovariation. Eine Korrelationsanalyse nach Bravais-Pearson ist jedoch nur bei linearen Zusammenhängen anwendbar.
Bei einer Korrelation wird der ungerichtete lineare Zusammenhang zweier Variablen untersucht. „Ungerichtet“ bedeutet, dass nicht von einer abhängigen und einer unabhängigen Variable gesprochen wird. Es werden folglich keine kausalen Aussagen gemacht.
Oft werden auch die Begriffe „Produkt-Moment-Korrelation“ oder „Pearson-Korrelation“ für den Korrelationskoeffizienten nach Bravais und Pearson verwendet. Etwas ungenau wird auch schlicht von einer „Korrelation“ oder einer „bivariaten Korrelation“ gesprochen. Dies ist problematisch, zumal es eine grosse Anzahl an verschiedenen Korrelationskoeffizienten gibt, wie beispielsweise die Rangkorrelation nach Spearman für ordinale Variablen.
Die Fragestellung einer Korrelation wird oft so verkürzt:
„Gibt es einen Zusammenhang zwischen zwei Variablen?“
1.1. Beispiele für mögliche Fragestellungen
- Gibt es einen Zusammenhang zwischen Sportlichkeit und Alter?
- Eine Gruppe Studierender löst zwei verschiedene IQ-Tests. Gibt es einen Zusammenhang zwischen den Resultaten der beiden Tests?
- Besteht ein Zusammenhang zwischen PC-Kenntnissen und der täglichen Internetnutzung?
- Gibt es einen Zusammenhang zwischen dem Schädlingsbefall einer Pflanzenart und Anzahl Regentage?
1.2. Voraussetzungen
| ✓ | Die Variablen sind mindestens intervallskaliert |
| ✓ | Die Variablen sind normalverteilt |
| ✓ | Der untersuchte Zusammenhang zwischen den Variablen muss linear sein |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
Medienwissenschaftler wollen herausfinden, ob es einen Zusammenhang gibt zwischen dem Konsum von Ego-Shooter-Spielen (Spielzeit in Stunden pro Woche) und der Gewaltbereitschaft (erhoben auf einer Skala von 0-50) bei Jugendlichen.
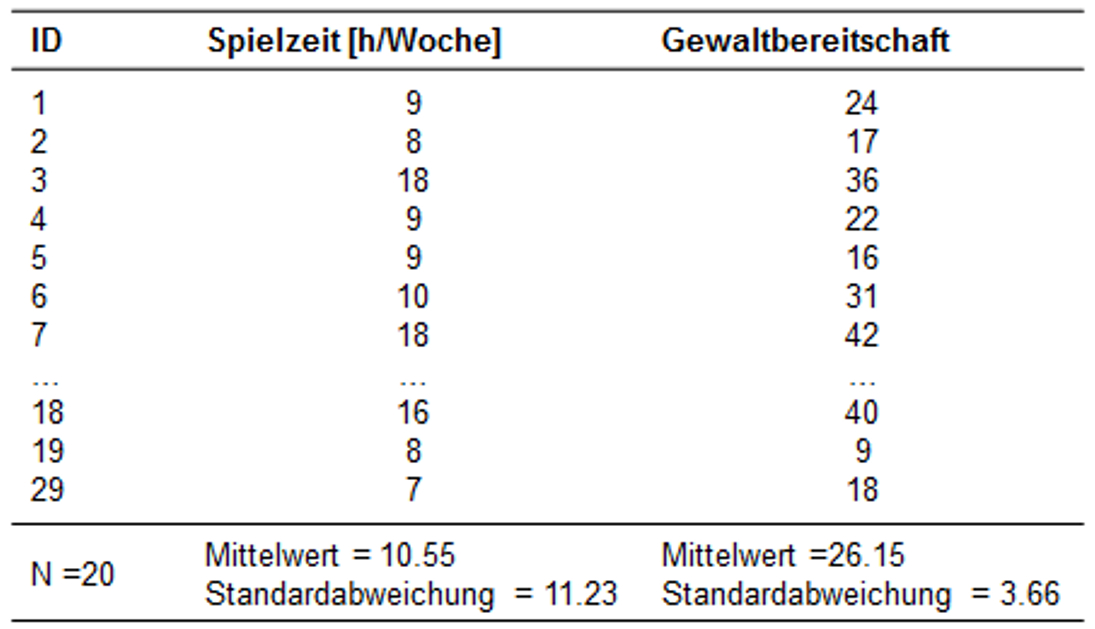
Der zu analysierende Datensatz enthält zu Beginn neben der Probandennummer (ID), die Variablen Spielzeit und Gewaltbereitschaft.
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Grafische Veranschaulichung des Zusammenhangs
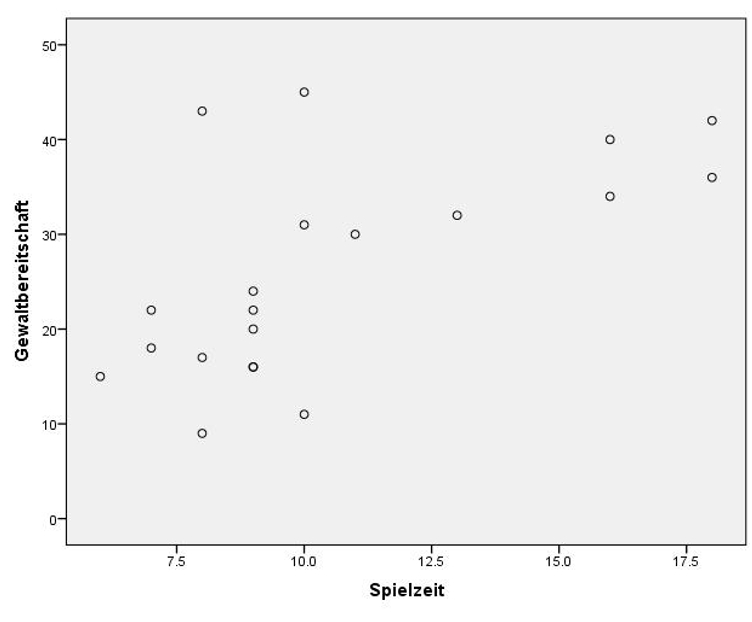
Um visuell zu prüfen, ob ein linearer Zusammenhang vorliegen könnte, empfiehlt es sich vorab ein Streudiagramm („Scatterplot“) zu erstellen. Mit SPSS lässt sich ein solches mit dem folgenden Befehl erzeugen:
Grafik > Diagrammerstellung > Streu-/Punkt-Diagramm > Einfaches Streudiagramm.
Das Streudiagramm in Abbildung 3 zeigt eine tendenziell positive lineare Beziehung zwischen den beiden Variablen. Das heisst, die beiden Variablen korrelieren vermutlich. Da die Korrelationsanalyse einen ungerichteten Zusammenhang untersucht, lässt er sich auf zwei Weisen ausformulieren: Je länger jemand Ego-Shooter-Games spielt, desto höher ist die Gewaltbereitschaft. Je höher die Gewaltbereitschaft, desto länger spielt jemand Ego-Shooter.
2.3. Berechnung des Korrelationskoeffizienten
Um die „Enge“ dieses Zusammenhangs erfassen zu können, wird der Korrelationskoeffizient r nach Bravais-Pearson berechnet.
mit
Der Korrelationskoeffizient kann nur Werte im Bereich zwischen -1 und +1 annehmen. Ist er kleiner als Null (r < 0), so besteht ein negativer linearer Zusammenhang. Bei einem Wert grösser als Null (r > 0) besteht ein positiver linearer Zusammenhang und bei einem Wert von Null (r = 0) besteht kein Zusammenhang zwischen den Variablen.
Im nächsten Schritt muss geprüft werden, ob sich der Korrelationskoeffizient signifikant von 0 unterscheidet. Mit dem Korrelationskoeffizienten alleine lässt sich noch keine Aussage darüber machen, ob ein signifikanter Zusammenhang zwischen den beiden Variablen besteht oder nicht. Ob ein Korrelationskoeffizient signifikant ist, hängt unter anderem von der Stichprobengrösse ab. So genügt bei einer grossen Stichprobe bereits ein kleiner Korrelationskoeffizient für ein signifikantes Ergebnis, während dies bei einer kleinen Stichprobe nicht der Fall ist. Getestet wird die Signifikanz mit SPSS.
3. Korrelation mit SPSS
3.1. SPSS-Befehle
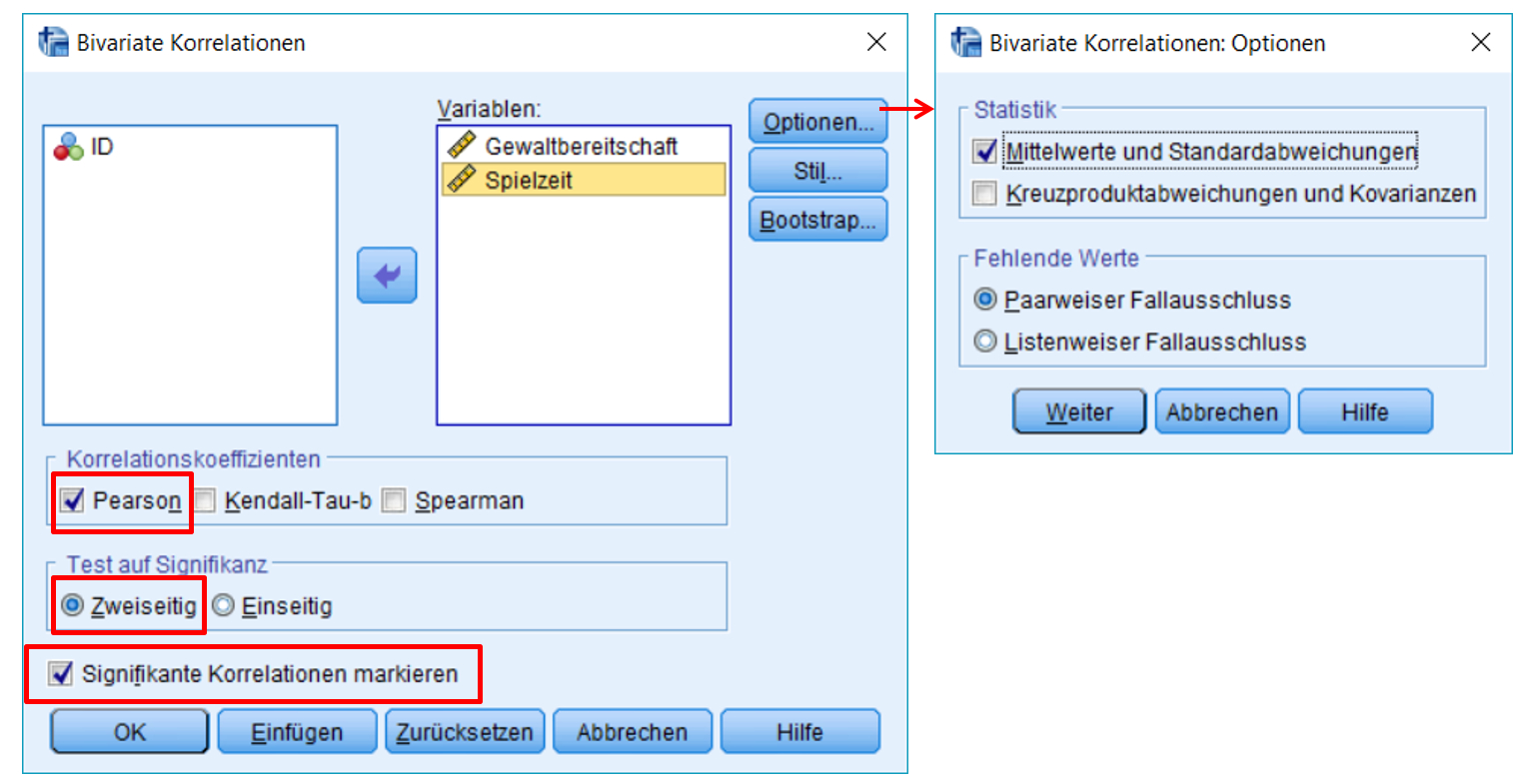
SPSS-Menü: Analysieren > Korrelation > Bivariat
Hinweise
- Unter Test auf Signifikanz wird zweiseitig gewählt, da ein ungerichteter Zusammenhang angenommen wird.
- Zusätzlich lässt sich festlegen, dass signifikante Korrelationen markiert werden sollen. Hierbei ist jedoch zu beachten, dass SPSS eventuell ein anderes Signifikanzniveau voraussetzt, als gewünscht wird. Was SPSS macht, zeigt eine Fussnote an der Korrelationstabelle.
- Werden mehrere Korrelationen gleichzeitig berechnet, so muss entschieden werden, wie fehlende Werte behandelt werden sollen: Paarweiser Fallausschluss bedeutet, dass für jede Korrelation alle Fälle verwendet werden, die für beide Variablen gültige Werte aufweisen. Damit kann n je nach Variablenpaar unterschiedlich sein. Listenweiser Fallausschluss bedeutet, dass für alle Korrelationen die gleichen Fälle verwendet werden – jene Fälle, die für alle Variablen in der Analyse gültige Fälle aufweisen.
SPSS-Syntax
CORRELATIONS
/VARIABLES= Gewaltbereitschaft Spielzeit
/PRINT=TWOTAIL NOSIG
/STATISTICS DESCRIPTIVES
/MISSING=PAIRWISE.
3.2. Deskriptive Statistik
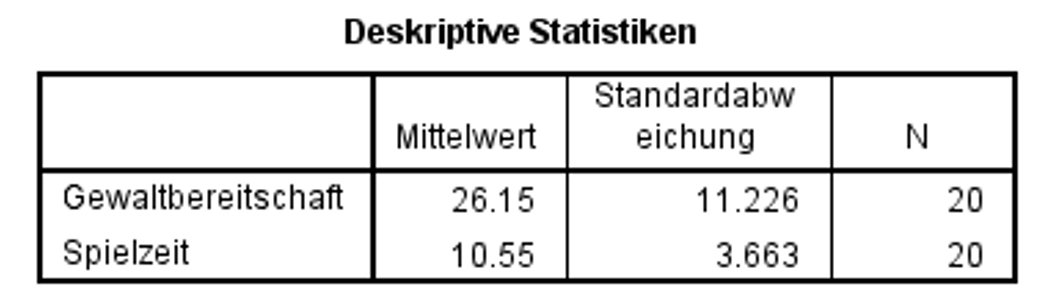
Abbildung 5 können die Mittelwerte und Standardabweichungen der Variablen Gewaltbereitschaft und Spielzeit abgelesen werden. Im Mittel liegt die Gewaltbereitschaft der Jugendlichen bei 26.15. Die wöchentliche Spielzeit liegt durchschnittlich bei 10.55 Stunden.
3.3. Ergebnisse der Korrelationsanalyse
Der SPSS-Output in Abbildung 6 gibt den Korrelationskoeffizienten sowie den p-Wert (Signifikanz) und die Stichprobengrösse n wieder. Es wird ersichtlich, dass ein Zusammenhang vorliegt zwischen Gewaltbereitschaft und Spielzeit (r = .628, p = .003, n = 20). Da r einen positiven Wert aufweist, kann von einem positiven linearen Zusammenhang zwischen Spielzeit und Gewaltbereitschaft ausgegangen werden. Das bedeutet: Je länger gespielt wird, desto höher ist die Gewaltbereitschaft bei Jugendlichen; respektive je höher die Gewaltbereitschaft, desto länger wird gespielt.
Die Werte auf der Diagonalen der Tabelle zeigen den Zusammenhang jeder Variable mit sich selbst. Diese Korrelation beträgt stets 1, da jede Variable perfekt mit sich selbst korreliert ist.
3.4. Berechnung des Bestimmtheitsmasses
Wird dieser Wert mit 100 multipliziert, so ergibt sich ein Prozentwert. Dieser gibt an, welcher Anteil der Varianz in beiden Variablen durch gemeinsame Varianzquellen determiniert wird. Für das vorliegende Beispiel beträgt der Anteil der gemeinsamen Varianz 39.4%.
3.5. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel ist die Korrelation der beiden Variablen signifikant, doch es stellt sich die Frage, ob der Zusammenhang gross genug ist, um ihn als bedeutend einzustufen. Der Korrelationskoeffizient r von Bravais-Pearson stellt selbst ein Mass für die Effektstärke dar.
Um zu bestimmen, wie gross der gefundene Zusammenhang ist, kann man sich an der Einteilung von Cohen (1992) orientieren:
r = .10 entspricht einem schwachen Effekt
r = .30 entspricht einem mittleren Effekt
r = .50 entspricht einem starken Effekt
Damit entspricht ein Korrelationskoeffizient von .628 einem starken Effekt.
3.6. Eine typische Aussage
Die wöchentliche Spielzeit von Ego-Shooter-Spielen und die Gewaltbereitschaft korrelieren signifikant (r = .628, p = .003, n = 20). Je länger eine Person Ego-Shooter Games spielt, desto gewaltbereiter ist sie, oder je gewaltbereiter jemand ist, desto länger spielt die Person Ego-Shooter-Spiele. Dabei handelt es sich nach Cohen (1992) um einen starken Effekt.