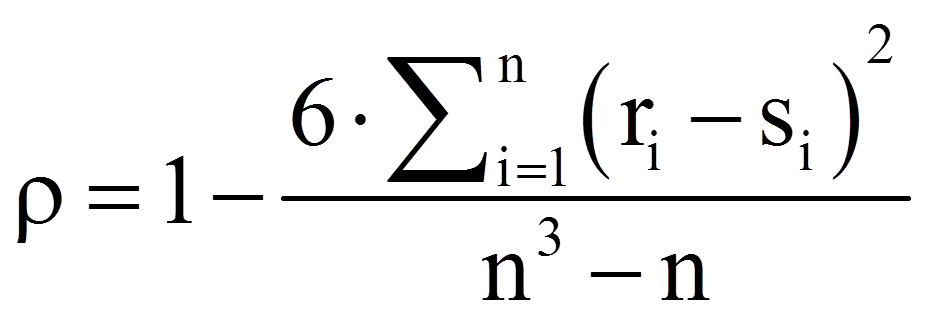 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Korrelationskoeffizienten
3. Korrelation mit SPSS
3.1. SPSS-Befehle
3.2. Ergebnisse der Rangkorrelationsanalyse
3.3. Berechnung des Bestimmtheitsmasses
3.4. Berechnung der Effektstärke
3.5. Eine typische Aussage
Quick Start
| Wozu wird eine Rangkorrelation verwendet? Die Rangkorrelationsanalyse nach Spearman berechnet den linearen Zusammenhang zweier mindestens ordinalskalierter Variablen. SPSS-Menü
Analysieren > Korrelation > Bivariat SPSS-Syntax
NONPAR CORR /VARIABLES= Variablen /PRINT=SPEARMAN TWOTAIL NOSIG SPSS-Beispieldatensatz
Rangkorrelation |
1. Einführung
Die Rangkorrelationsanalyse nach Spearman berechnet den linearen Zusammenhang zweier mindestens ordinalskalierter Variablen.
Da stets der Zusammenhang zwischen zwei Variablen untersucht wird, wird von einem „bivariaten Zusammenhang“ gesprochen.
Zwei Variablen hängen dann linear zusammen, wenn sie linear miteinander variieren (also kovariieren). Sie können dies in unterschiedlicher Weise tun:
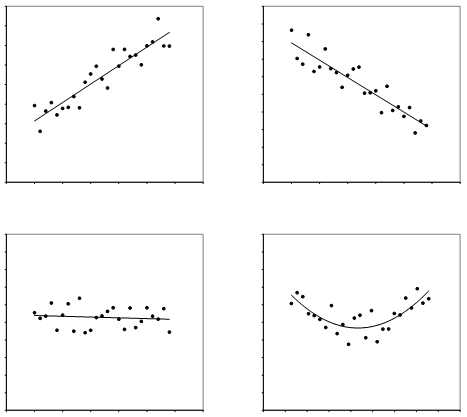
- Gleichsinnige oder positive Korrelation: Hohe (tiefe) Ausprägungen der einen Variablen gehen mit hohen (tiefen) Ausprägungen der zweiten Variablen einher (Abbildung 1: oben links). Zum Beispiel: Je besser die Mathematiknote eines Lernenden, desto zufriedener ist er mit seiner Leistung. Je schlechter die Mathematiknote, desto geringer ist die Zufriedenheit.
- Gegenläufige oder negative Korrelation: Hohe Werte der einen Variablen gehen mit tiefen Werten der anderen einher (Abbildung 1: oben rechts). Zum Beispiel: Je höher das Medianeinkommen eines Landes ist, desto tiefer ist die Arbeitslosigkeit. Je tiefer das Medianeinkommen ist, desto höher ist die Arbeitslosigkeit.
Auch nicht-lineare Zusammenhänge sind möglich, wie beispielsweise eine u-förmige (Abbildung 1: unten rechts) oder umgekehrt u-förmige Kovariation. Eine Rangkorrelationsanalyse ist jedoch nur bei linearen Zusammenhängen anwendbar.
Bei der Rangkorrelation wird der ungerichtete lineare Zusammenhang zweier Variable untersucht. „Ungerichtet“ bedeutet, dass nicht von einer abhängigen und einer unabhängigen Variable gesprochen wird. Es werden folglich keine kausalen Aussagen gemacht.
Die Rangkorrelation nach Spearman ist das nichtparametrische Äquivalent der Korrelationsanalyse nach Bravais-Pearson und wird angewandt, wenn die Voraussetzungen für ein parametrisches Verfahren nicht erfüllt sind. Nicht-parametrische Verfahren sind auch bekannt als „voraussetzungsfreie Verfahren“, weil sie geringere Anforderungen an die Verteilung der Messwerte in der Grundgesamtheit stellen. So müssen die Daten nicht normalverteilt sein und die Variablen müssen lediglich ordinalskaliert sein. Auch bei kleinen Stichproben und Ausreissern kann eine Rangkorrelation berechnet werden.
Oft werden auch die Begriffe „Spearman-Korrelation“ oder „Spearmans Rho“ verwendet, wenn von einer Rangkorrelation nach Spearman gesprochen wird.
Die Fragestellung einer Rangkorrelation wird oft so verkürzt:
„Gibt es einen Zusammenhang zwischen zwei Variablen?“
1.1. Beispiele für mögliche Fragestellungen
- Gibt es einen Zusammenhang zwischen der Einschätzung der eigenen Risikobereitschaft mit der Einschätzung der Risikobereitschaft durch die Eltern?
- Besteht ein Zusammenhang zwischen dem Preis einer 1-Liter-Wasserflasche und der Distanz zum Universitätsgebäude?
- Besteht ein Zusammenhang zwischen dem Alter eines Autos und dem Bremsweg?
- Zeigt sich ein Zusammenhang zwischen der Anzahl technischer Pannen bei Computer-Usern in einer Firma und den Verkaufszahlen eines nahegelegenen Likörladens?
1.2. Voraussetzungen
| ✓ | Die Variablen sind mindestens ordinalskaliert |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
Ein neues Messinstrument soll die Risikobereitschaft von Studienabgängern messen (Skala 0-100). Nun soll untersucht werden, ob die Selbsteinschätzung der Risikobereitschaft bei den Studienabgängern mit der Fremdeinschätzung durch deren Partner/Partnerin (Skala 0-10) zusammenhängt.
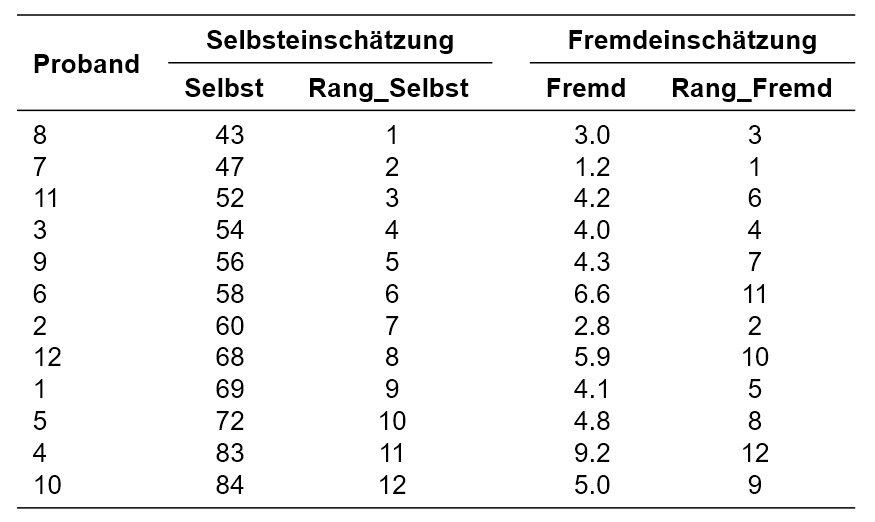
Der zu analysierende Datensatz enthält zu Beginn neben der Probandennummer (Proband) die Variablen Selbst und Fremd.
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Korrelationskoeffizienten
Die Rangkorrelation basiert auf der Idee der Rangierung der Daten. Das heisst, es wird nicht mit den Messwerten selbst gerechnet, sondern diese werden durch Ränge ersetzt, mit welchen der eigentliche Test durchgeführt wird. Damit beruht die Berechnung des Tests ausschliesslich auf der Ordnung der Daten (grösser als, kleiner als). Die absoluten Abstände zwischen den Werten werden nicht berücksichtigt.
Um die Messwerte mit Rängen zu versehen, werden zunächst die einzelnen Messwerte der beiden Variablen gemäss ihrer Grösse (von den kleinsten Werten aufsteigend) aufgereiht (siehe beispielsweise Abbildung 1, Spalte „Selbst“). Danach wird für beide Variablen je eine Rangreihe gebildet, wobei hierfür ebenfalls die Ränge aufsteigend gekennzeichnet werden (von 1 ausgehend und aufsteigend) (siehe beispielsweise Abbildung 1, Spalte „Rang_Selbst“). Kommt ein Messwert mehrfach vor (engl. „ties“), so werden sogenannte „verbundene Ränge“ gebildet. Wenn beispielsweise Rang 5 und 6 beide die gleichen Messwerte aufweisen, wird aus diesen beiden der Mittelwert gebildet ((5 + 6)/2 = 5.5) und die Ränge 5 und 6 werden neu beide mit dem Rang 5.5 versehen.
Der Korrelationskoeffizient ρ (rho) nach Spearman wird anschliessend anhand der folgenden Formel berechnet:
mit
| = | Rangplatz innerhalb der Variable X des i-ten Probanden | |
| = | Rangplatz innerhalb der Variable Y des i-ten Probanden | |
| = | Anzahl Probanden |
Diese Formel wird allerdings lediglich angewendet, wenn keine verbundenen Rangplätze vorhanden sind. Bei verbundenen Rangplätzen wird die Formel deutlich komplexer.
Die Rangkorrelation kann auch berechnet werden, indem eine Korrelation nach Bravais-Pearson für die Ränge der beiden Variablen berechnet wird.
Der Rangkorrelationskoeffizient ρ kann Werte zwischen -1 und 1 annehmen. Ist er kleiner als Null (ρ < 0), so besteht ein negativer linearer Zusammenhang. Bei einem Wert grösser als Null (ρ > 0) besteht ein positiver linearer Zusammenhang und bei einem Wert von Null (ρ = 0) besteht kein Zusammenhang zwischen den Variablen.
3. Korrelation mit SPSS
Hinweise
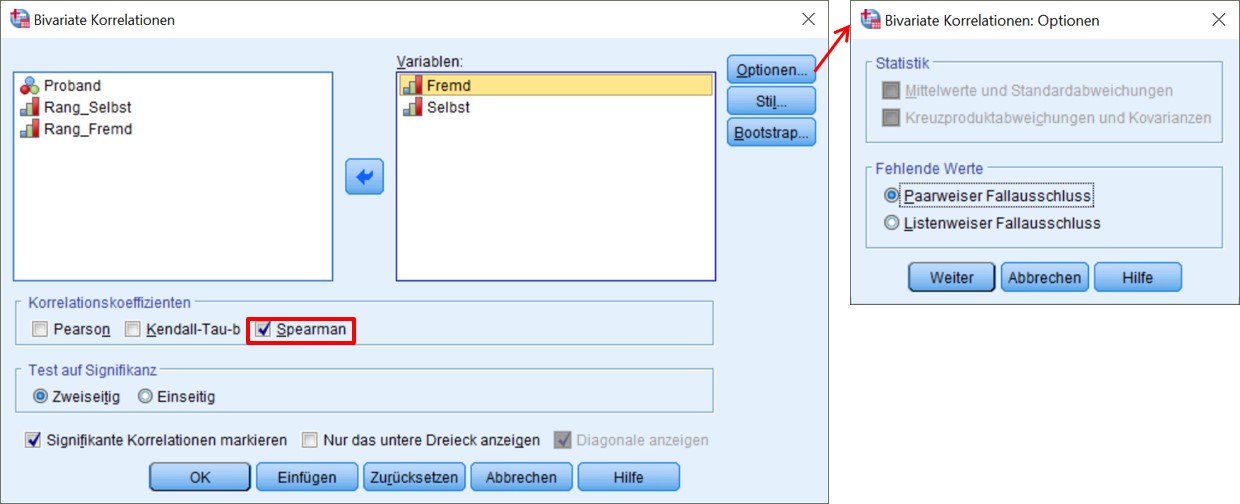
- Da es sich um ordinalskalierte Variablen handelt, wird unter „Korrelationskoeffizienten“ Spearman gewählt.
- Unter „Test auf Signifikanz“ wird zweiseitig gewählt, da ein ungerichteter Zusammenhang angenommen wird.
- Zusätzlich lässt sich festlegen, dass signifikante Korrelationen markiert werden sollen. Hierbei ist jedoch zu beachten, dass SPSS eventuell ein anderes Signifikanzniveau voraussetzt, als gewünscht wird. Was SPSS macht, zeigt eine Fussnote an der Korrelationstabelle.
- Werden mehrere Korrelationen gleichzeitig berechnet, so muss entschieden werden, wie fehlende Werte behandelt werden sollen: Paarweiser Fallausschluss bedeutet, dass für jede Korrelation alle Fälle verwendet werden, die für beide Variablen gültige Werte aufweisen. Damit kann n je nach Variablenpaar unterschiedlich sein. Listenweiser Fallausschluss bedeutet, dass für alle Korrelationen die gleichen Fälle verwendet werden – jene Fälle, die für alle Variablen in der Analyse gültige Fälle aufweisen.
- Bei ordinalskalierten Variablen kann auf „Statistiken“ verzichtet werden.
SPSS-Syntax
NONPAR CORR
/VARIABLES= Fremd Selbst
/PRINT=SPEARMAN TWOTAIL NOSIG
/MISSING=PAIRWISE.
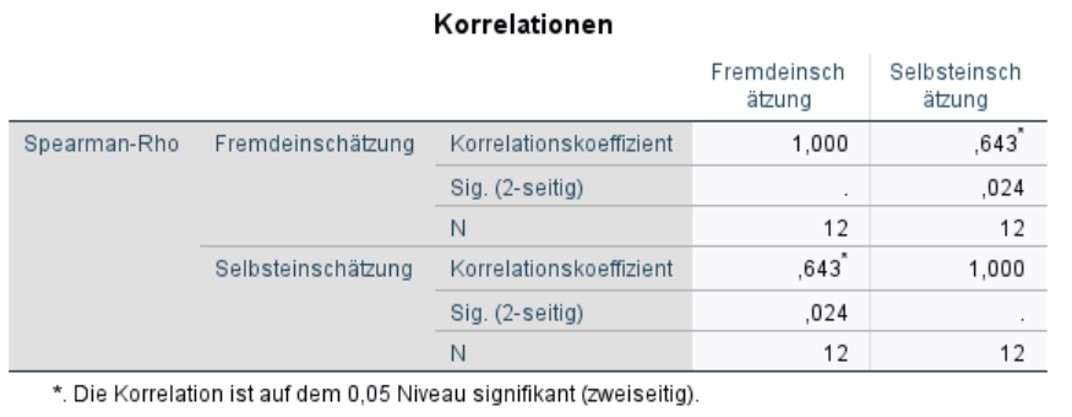
SPSS gibt die Teststatistik, den Korrelationskoeffizienten von Spearman, aus: Abbildung 4 zeigt, dass die Korrelation zwischen Selbst- und Fremdeinschätzung bei rs = .643 liegt. Der p-Wert beträgt .024. Somit ist die Korrelation statistisch signifikant (p < .05). Das positive Vorzeichen des Korrelationskoeffizienten lässt erkennen, dass es sich hierbei um eine gleichsinnige Beziehung der beiden Variablen handelt. Dies bedeutet, dass höhere Werte in der Selbsteinschätzung mit höheren Werten in der Fremdeinschätzung einhergehen (rs = .643, p = .024, n = 12).
Die Werte auf der Diagonalen der Tabelle zeigen den Zusammenhang jeder Variable mit sich selbst. Diese Korrelation beträgt stets 1, da jede Variable perfekt mit sich selbst korreliert ist.
3.3. Berechnung des Bestimmtheitsmasses
Wird dieser Wert mit 100 multipliziert, ergibt sich ein Prozentwert. Dieser gibt an, welcher Anteil der Varianz in beiden Variablen durch gemeinsame Varianzquellen determiniert wird. Für das vorliegende Beispiel beträgt der Anteil der gemeinsamen Varianz 41.3%.
3.4. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel ist die Korrelation der beiden Variablen signifikant, doch es stellt sich die Frage, ob der Zusammenhang gross genug ist, um ihn als bedeutend einzustufen. Der Korrelationskoeffizient r von Spearman ist ein Mass für die Effektstärke.
Um zu bestimmen, wie gross der gefundene Zusammenhang ist, kann man sich an der Einteilung von Cohen (1992) orientieren:
r = .10 entspricht einem schwachen Effekt
r = .30 entspricht einem mittleren Effekt
r = .50 entspricht einem starken Effekt
Damit entspricht ein Korrelationskoeffizient von .643 einem starken Effekt.
3.5. Eine typische Aussage
Die Selbsteinschätzung der Studienabgängern bezüglich ihrer Risikobereitschaft korreliert signifikant mit der Fremdeinschätzung durch ihre Partner, rs = .643, p = .024, n = 12. Dabei handelt es sich nach Cohen (1992) um einen starken Effekt.